News
Protein-ligand binding affinity is one of the most useful metrics for predicting drug activity. Techniques for estimating binding affinity are undergoing constant development and change, yet one thing remains constant - the centrality of non-covalent interactions. How to best predict these interactions is one of the hottest and most challenging fields in theoretical biochemical research, with new approaches developed on a near weekly basis, ranging from totally empirical, e.g., 1, to the almost completely ab-initio, e.g., 2. The rise of machine learning techniques over the past year has already transformed many areas of drug discovery, and prediction of non-covalent interactions is no exception. Below we present one of the most promising approaches in this field, compare it to Cresset’s existing methodology, and discuss what this means for future Cresset software development.
Before diving into a discussion of these new developments it’s worth taking a moment to consider the concept of Electrostatic Complementarity™ (EC) 3, what is it, how to calculate it and why it is relevant to drug design. The EC of a ligand is measure of how well the electrostatic profile of the ligand matches up with the electrostatic profile of the pocket to which you want it to bind. If the EC is high, then wherever the electrostatic potential (ESP) surface of the ligand is positive there will be a corresponding negative charge on the ESP surface of the protein, and vice versa. In other words, if the EC is high, then the non-covalent interactions between the protein and ligand are energetically favorable whilst EC doesn’t necessarily directly predict binding affinity, we have found very good correlation, particularly within a congeneric series of ligands, between EC score and activity.
To determine the EC of a ligand we usually need to first determine the ESP surfaces for the ligand and the protein, which in turn requires we know the charge distribution of the ligand/protein. Unfortunately, predicting the charge distribution ab initio, e.g., by using the electron density from a post-Hartree-Fock calculation, is too computationally demanding for it to be practically useful for virtual screening. Consequently, approximate charge models are usually employed. Cresset uses its own XED force field 4, which has been shown to be highly efficient and accurate 5. Yet science does not stand still, and in this post, we ask whether XED is still the best choice.
A dizzying number of alternatives exist, from full electron density methods like RESP 6, atomic charge models like AM1-BCC 7, to multipole methods like AMOEBA 8. Perhaps one of the most exciting is a charge model recently developed by Astex Pharmaceuticals 9, hereafter referred to as the Astex-DNN. This is similar to XED in many ways; it defines the charge distribution of a molecule by assigning charges to points within the molecule, one to each of the atoms, and several more to ‘feature points’ in the molecule. These feature points are: approximate positions of lone pairs, sigma holes, pi-orbitals, etc. Yet the Astex DNN differs from XED in a key respect; whereas the XED force field was developed through a mix of chemical intuition and refinement of charge parameters through comparison against experimental data, the charges of the Astex-DNN are determined using a dynamic neural network (DNN) trained to assign charges which reproduce ESP surfaces obtained from high-level second-order Moller-Plesset calculations. So, in essence, we have a heuristic model (XED) and a statistical model (Astex-DNN). Whilst heuristic models have the advantage of being more comprehensible, the latter may well outperform them on more ‘exotic’ molecules for which standard chemical heuristics fail. Furthermore, improvements of the Astex-DNN may not require any significant chemical insight or modification of the model; one simply needs to expand the data set used to train the DNN and retrain the model.
To compare the performance of the Astex-DNN and XED models we ask four main questions:
The Astex-DNN and XED models assign charges to points on the atoms, as well as to non-atomic points located at significant positions in the electronic structure. Whilst the location of the atomic points is necessarily the same for both models, the positions and number of non-atomic points differs. Figure 1 shows both XED and the Astex-DNN agree on the approximate location of the non-atomic points, with a few key differences. the XED model places these points significantly closer to the atoms than the Astex-DNN model. Furthermore, they use different numbers of charge points for certain features of the electronic structure, e.g., XED uses multiple non-atomic charge points to describe lone pairs, whereas the Astex-DNN uses just one.
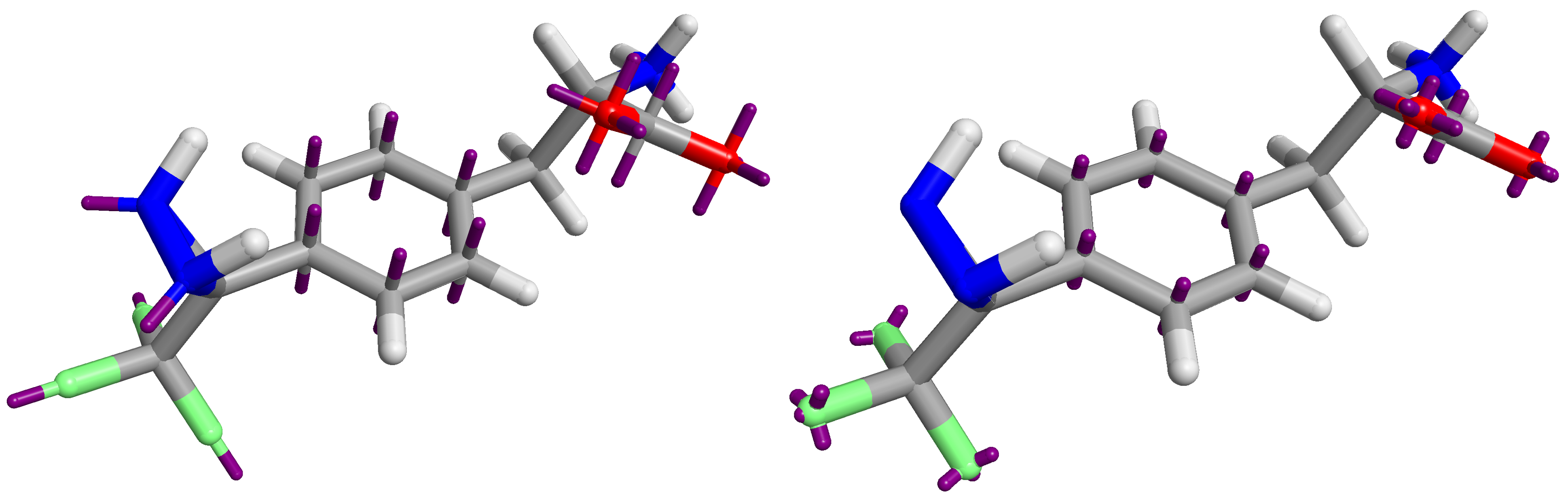
Left: Figure 1a (Astex-DNN). Right: Figure 1b (XED). Purple lines indicate the location of non-atomic charge points.
The difference in the position of the non-atomic charge points makes a direct quantitative comparison of the charge values assigned to the charge points moot, but from the comparison of the electrostatic potential maxima we can see the models appear to be remarkably similar (Figure 2).
Comparison of the ESP surfaces is useful as disagreement indicates that at least one of the models is incorrect and could indicate shortcomings of the models. Given that the models use different sets of non-atomic charge points the predicted ESP surfaces will almost certainly differ; the only case in which they would not is in rare cases of symmetry, or when the charges on the non-atomic points were zero. Yet despite this key difference we found the predicted ESP surfaces to be surprisingly similar, although the Astex-DNN does predict a slightly greater degree of polarization. A typical example is shown in Figures 3a and 3b.
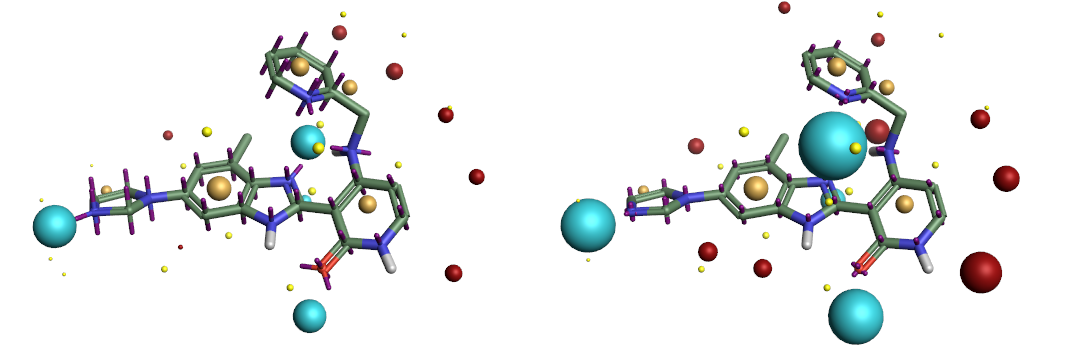
Left: Figure 2a (Astex-DNN). Right: Figure 2b (XED). Illustration of the electrostatic potential obtained using the two charge models. Spheres are ‘field points’ indicating maxima and minima in the electrostatic potential.
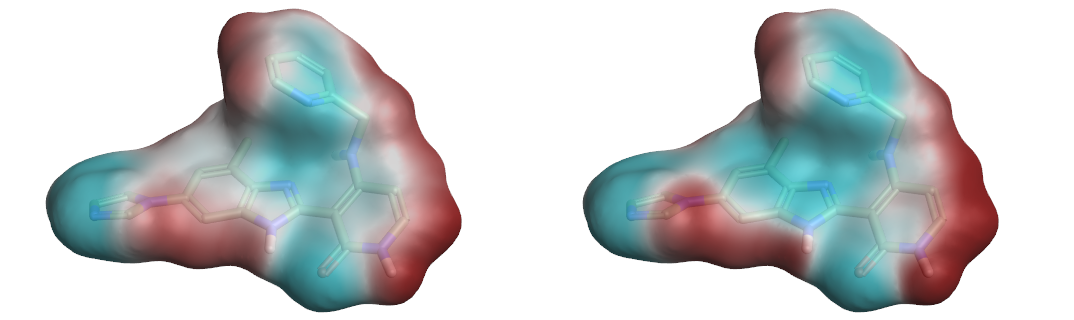
Left: Figure 3a (Astex-DNN). Right: Figure 3b (XED). ESP surfaces calculated using the two different charge models.
As such calculations play a vital role in virtual screening techniques, an interesting test is to see how well the two models perform in ligand alignment calculations. This test asks the following question: If we know the electrostatic profile of two ligands, A and B, both of which are known to bind to a protein, can we determine the bioactive conformation of one of these ligands from the bioactive conformation of the other?
To answer this question we require two experimental structures, one where a protein is bound to ligand A, and another where the same protein is bound to ligand B. The first step is to align these two structures. This will inform on how the bioactive conformation of ligand A aligns with the bioactive conformation of ligand B. We call this the ‘correct’ alignment.
A large number of conformers of ligand B are generated, and we attempt to align each of these conformers with the bioactive conformation of ligand A. Crucially, this alignment is not based on the atomic structure of the two conformations, and relies solely on the similarity in the electrostatic profiles. Hence the conformer of ligand B which aligns ‘best’ with the bioactive conformer of ligand A will be the one where the electrostatic profiles of the two conformers have the greatest overlap. We then compare the structure of the ‘best’ conformation of ligand B, which we obtained through comparison of electrostatic profiles, with the ‘correct’ structure of ligand B, which we obtained through comparison of the structure of the protein-ligand complexes. This structural comparison is done by calculating the root mean squared difference (RMSD) of the atomic positions of these two conformations of ligand B. If the RMSD is low it indicates electrostatic similarity is a useful tool in for identifying the bioactive conformation of a ligand. As the electrostatic similarity is determined from the electrostatic profiles, which are in turn determined from the charge model, this test will serves to answer the question of which of the two charge models is best when attempting to identify the bioactive conformations of a ligand.
In an ideal world these two structures of ligand B would be identical, but this is practically never the case. The first reason being that the electrostatic profile of a ligand does not uniquely determine a single conformation, and that even quite large variations in the atomic structure can have comparatively little impact on the electrostatic profile. Second is that our sampling of the conformational space is inevitably incomplete, so the bioactive conformation of ligand B may not be amongst the set of conformations we have generated. Third, there is no guarantee that ligand A and ligand B have the same binding mode, even if they bind to the same pocket. If this is the case then the conformation of B which has an electrostatic profile most similar to the bioactive conformation of A may not be the conformation B takes when bound in the protein pocket. Despite these drawbacks this is a very useful test, as it directly parallels the real-world use of these charge models.
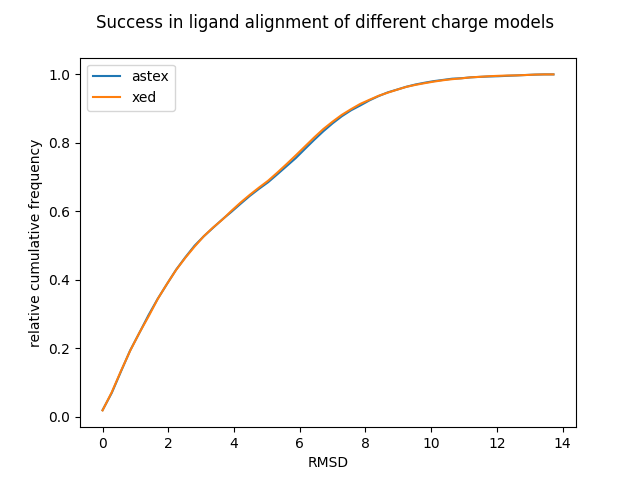
Figure 4: Relative cumulative frequency plot indicating the performance of the two charge models in ligand alignment calculations.
Figure 4 shows a cumulative frequency plot of the RMSD between the bioactive conformation and the conformation with the highest EC score for the Astex-DNN and XED charge models. The more conformations with a low RMSD, the better. This test was carried out on 119 proteins and ~1450 ligands obtained from the AstraZeneca/Cambridge Crystallographic Data Centre 10.
The two models perform very similarly, unnervingly so. However, there were numerous clear discrepancies in the results, but this is obscured by the very large size of the dataset. Neither model is 100% accurate. This is to be expected; slight variations in the geometry of the bioactive conformation will not have significant impact on the strength of ligand protein binding. Furthermore, it was interesting to note that on closer examination of the results both charge models had similar failure cases, i.e., if the incorrect conformation was predicted using one charge model, then it was likely to also be incorrectly predicted in the other.
The tests conducted indicate that the XED and Astex-DNN charge models show very similar performance, and that either one would be a good choice for use in virtual screening calculations. In some respects, this is disappointing, as it indicates despite the huge advances in machine learning techniques, complex neural networks still do not outperform heuristic algorithms based on human intuition. On the other hand, it is highly reassuring, as it indicates that the intuitions and concepts used to build the original XED force field were correct.
The lack of clear distinction between the two models by no means represents an impasse in the development of charge models. First, application of machine learning techniques to drug discovery is currently in its infancy, and we can expect many more exciting developments to come. Indeed, development of a model capable of equalling the performance of the XED force field, without relying on the heuristics of chemical theory, is a remarkable accomplishment. It is possible by simple extension of the dataset used to train the model that it would be possible to obtain one which outperformed XED. However, there is a more interesting avenue for progress to be discussed.
One class of ligands which both XED and the Astex-DNN perform poorly on is charged ligands. A key reason for this is that if a molecule features a charged atom, then the ESP surface obtained from a DFT calculation in vacuo will be completely dominated by this charge. This is not a fault in the DFT calculation; it is an accurate representation of the ESP surface, but the lack of distinguishing features of such monotonous ESP surfaces means that ligand alignment calculations are hard to perform accurately. Essentially, the ESP surfaces of charged ligands of a similar size and shape all end up looking much the same, preventing it from being used to determine which ligands will bind to a protein and which won’t. Fortunately, the origins of this issue are clear. The DFT calculations used to generate training data for the Astex model were performed in vacuum; when what we are really interested is: what is the ESP surface of the ligand when it is in the binding pocket. Interactions between the ligand and the pocket can result in the formal charge becoming more localized on specific groups within the molecule, and a decrease in the overall charge on the ligand. Therefore, if we are to perform ligand alignment calculations on charged ligands, we need to know what these ligand-pocket interactions are, and how they affect the ESP of the ligand.
Unfortunately, the nature of such interactions is hard to predict. Whilst we can assume that if there is a charged group on the ligand, then there must be an oppositely charged group at a complementary point within the pocket, it is not clear how to determine what the strength of the charge on this point should be in order to correctly represent the protein-ligand interaction. This is in many respects due to the shortcomings of using ESP surfaces to describe protein-ligand binding. Whilst it is a good measure of the strength of the interaction between the two, it is by no means complete, and there are some important processes, e.g., hydrogen bonding, which will depend on the chemical composition of the two components.
At present, both the Astex-DNN and XED models use crude methods to tackle this issue. Both fundamentally rely on localizing the charge on the functional group and scaling the magnitude of this charge down by a factor in to ensure this charged group does not totally dominate the ESP profile. Given the ad hoc nature of these approaches they perform remarkably well, but alignment results for charged ligands remain more challenging than those for neutral ones. Improving this is a key challenge going forwards and is the subject of ongoing research at Cresset.
The pharmaceutical and biotech sectors suffer more data security breaches than any other industry, with 53% resulting from malicious activity. To protect against potential ...
Force fields provide critical infrastructure underlying a broad range of molecular modeling for drug discovery. Learn more in this recent ...
A chance to catch up on Professor Julien Michel's presentation at this recent Boston Area Group for Informatics and Modeling ...