Science
Robust science for results you can rely on
Introduction to Cresset technology
Our goal is to help you discover, design and optimize the best possible molecules for your project. We believe that computational methods are an excellent way of arriving at a better understanding of the properties and behaviors of chemical structures and proteins. Robust science is at the heart of everything we do. While we do prioritize scientific rigor, we also strive to be user-friendly and facilitate fast calculations for the user.
Cresset technology centers on the application of the eXtended Electron Distribution (XED) force field to the design of new small bioactive compounds. The XED approach improves traditional molecular mechanics by using a complex description of atoms to model charge away from atomic centers. This enables a more detailed description of electrostatics and excellent reproduction of intermolecular interactions. Developed by Dr Andy Vinter and refined by Cresset, the XED force field correctly models substituent effects on aromatics, charge density changes in complex aromatics and the intermolecular interactions of small molecules, water and proteins.
XED force field calculates excellent electrostatics
The most important factor affecting molecular recognition is electrostatics, but it is also affected by shape and hydrophobicity. Cresset’s approach describes the electrostatic environment around a ligand or protein as a molecular interaction potential (MIP) or field. The MIP describes all of the energetically important interactions that a ligand can make with a protein, and viewing the MIP of a protein provides clear insights as to why some ligands bind more strongly than others. Describing molecules in terms of electrostatics rather than structure, enables us to sensibly compare molecules from different series.
Electrostatic similarity calculations inform small molecule discovery
Cresset has a patented method to compare the molecular interaction potentials for two molecules and compute a similarity. Field similarity is used to:
- Design new molecules
- Scaffold hop to new areas of chemical space
- Understand and decipher SAR
- Find new lead structures
XED force field
Cresset’s main focus is the description of molecules in terms of electrostatics. For this to be effective, the electrostatic model needs to be accurate. Quantum mechanics calculations can give very accurate electrostatic potentials, but are still too slow in most cases. As a result, an accurate method of computing electrostatic potentials in a molecular mechanics context is needed.
Most standard force fields use the atom-centred charge (ACC) approximation: the electrostatics of the molecule are approximated by a set of point partial charges placed on the nuclei. Many methods are available to compute these partial charges (Gasteiger-Hückel, AM1-BCC, etc), but the underlying model is one point charge per atom. This method can work well for the gross long-distance electrostatic potential (e.g., dipole moments), but performs poorly when describing the electrostatic potential near the molecular surface. This is because atoms are not charged spheres: they have lone pairs, pi orbitals, sigma holes and so forth. In addition, atoms and molecules are polarizable and change their electrostatic behavior in response to external electric fields. The ACC model covers none of these effects. Newer force fields such as AMOEBA solve this problem by placing explicit multipoles and polarization functions on the atoms, which does give a much more realistic electrostatic potential. These force fields perform well on proteins but have issues with parameter transferability which makes them largely unsuitable for ligand modeling.
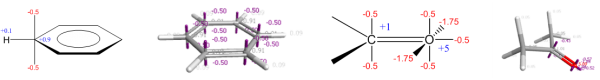
The XED force field was the first major effort to solve these electrostatic problems, and did so not by placing explicit multipoles on atoms but by placing additional monopoles around them. The technique was originally introduced by Hunter and Sanders, JACS 1989, to model aromatic-aromatic interactions, and was extended into a full general-purpose force field by Cresset’s founder Andy Vinter, JCAMD, 1994.
Additional monopole points, or XEDs (eXtended Electron Distributions), are treated within the force field as atoms with zero van der Waals radii. They are not placed in a rigid geometry with respect to their parent atom. Instead, they come with bond stretching and angle bending potentials and can move under the influence of external (and intramolecular) electrostatic potentials, allowing the direct modeling of polarizability. The more complex internal electrostatic model allows for intramolecular electrostatic/orbital interactions such as the anomeric effect to be modeled without the introduction of specific torsional parameters: the anomeric effect falls naturally out of the electrostatic model and does not need to be added post hoc.
The XED force field has been demonstrated to provide quantitatively superior results for the energetics of aromatic-aromatic interactions. Cresset’s academic collaborators have used the XED model to study and predict specific intermolecular interactions. For example, Professor Chris Hunter studied the dimerization of a series of di-aryl amides using NMR and computational chemistry (Substituent Effects on Aromatic Stacking Interactions). He found that the XED model accurately predicted the experimentally observed association constants.
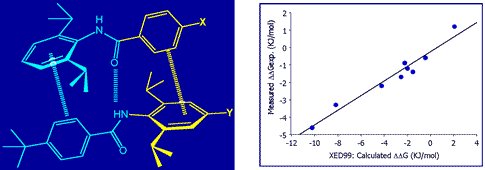
Dimerization of a series of di-aryl amides (left), experimentally observed association constants (right).
The superior modeling of aromatic interactions was used to design aromatic ‘zippers’ for linking collagen mimic fibres (Thrombogenic Collagen-Mimetic Peptides: Self-Assembly of Triple Helix-Based Fibrils Driven by Hydrophobic Interactions).
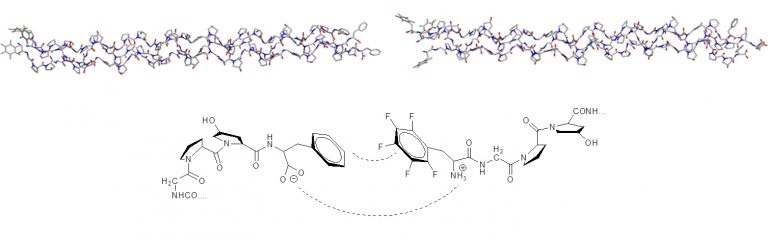
The XED force field provides both qualitatively and quantitatively correct results for the interaction of phenyl and pentafluorophenyl groups.
Over the last 20 years the XED force field has undergone numerous improvements. Unlike most other force fields, the XED force field is parameterised where possible against experimental data (microwave conformation energies, small molecule crystal structures etc.) rather than relying purely on ab initio calculations. XED 3, released in 2012 offers an improved treatment of nitrogen, amongst many other enhancements. Rather than having to assign separate types for trigonal and tetrahedral nitrogen, the XED 3 force field determines on the fly the degree of pyramidalization that is appropriate in any given molecular environment, allowing for a continuum from completely flat N to completely pyramidal N. In addition, XED 3 has an improved description of halogens, correctly describing the ‘sigma hole’ in the heavier halogens and giving good results for halogen bonding. Cresset continues to develop and improve the force field on an ongoing basis.

Calculating fields to assess molecular interactions
Cresset’s fundamental 3D ligand similarity technology compares molecules in terms of their molecular electrostatic interaction potentials (MIPs), or ‘fields’. The MIP of a molecule is a scalar field where the value at each point in space is the interaction energy of a charged probe atom (with the van der Waals parameters of oxygen) with the molecule. These are calculated using the XED force field. As the interaction energies are poorly defined inside the molecule, the field value is set to zero anywhere where the van der Waals interaction energy is positive and larger than the absolute value of the electrostatic energy.
Dealing with a full 3D scalar potential is computationally difficult. You can sample the values on a grid, but you then have issues with gauge variance, grid spacing and so forth leading to irreproducibility. Instead, what Cresset does is ask “Where are the maxima/minima of the fields?”. Each such extremum is termed a ‘field point’, and the set of field points is uniquely defined for any given molecular conformation. The field points are usually displayed as colored spheres, where the visual extent of each field point is determined by the magnitude of the field – stronger fields get larger spheres. This allows you to see at a glance where the molecule can make a locally maximal electrostatic interaction with another molecule. Full definitions of the fields and algorithm used to compute the field point positions are detailed in the paper Molecular Field Extrema as Descriptors of Biological Activity: Definition and Validation.
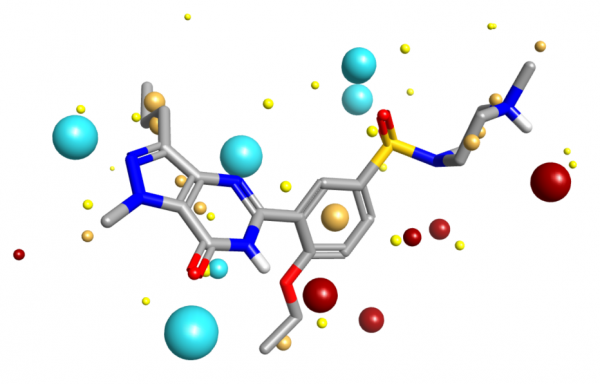
Molecular field extrema applied to Sildenafil extracted from PDB code 1UDT.
Cresset’s fields have been validated as part of the development of the the XED force field, and have also been extensively compared to experimental data from small molecule crystal structures. The distribution of H-bond donors and acceptors around a functional group is a good proxy for the interaction potential, and the field point patterns obtained are consistent with this information. Fields are also particularly useful for describing the properties of aromatic systems (building on the XED force field’s excellent description of these): the field surface around an aromatic ring holds a wealth of information about how electron rich/poor it is, how its charge density is arranged, and how strong a π-stacking interaction it could make. A few example rings are shown below.
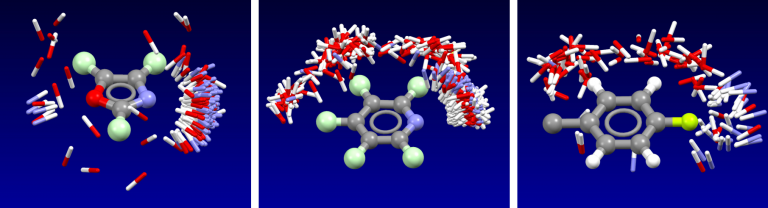
Isostar plot of oxazole, pyridine, fluorobenzene.
Whenever you are describing molecules in terms of electrostatics, it is critical to handle formal charge states correctly. Cresset have a complex rule-based system for assigning formal charges which, while not a complete pKa estimator, will correctly assign the protonation state for the vast majority of drug-like molecules at pH 7. However, just assigning the formal charge state is not enough. Solvation is much more important for ions than for neutral molecules, so additional effort needs to be made to account for that. See our full algorithm for handling formal charges in small molecules.
Fields on proteins
Cresset fields and field points have been extensively validated on small molecule structures. Extending this approach to proteins is more difficult, as much more attention needs to be paid to system preparation, charge states, and solvation effects. Flare, Cresset's ligand-based and structure-based drug design platform, solves these issues, in particular through careful protein preparation and the use of a modified dielectric function based on the work of Mehler (E. L. Mehler, The Lorentz-Debye-Sack theory and dielectric screening of electrostatic effects in proteins and nucleic acids, in Molecular Electrostatic Potentials: Concepts and Applications, Theoretical and Computational Chemistry Vol. 3, 1996).
The resulting interaction potentials (PIPs, or protein interaction potentials, to distinguish them from ligand MIPs) are extremely useful for analyzing a protein active site and determining what ligand properties might need to be altered to achieve optimum binding – see for example comparing ligand and protein electrostatics of Btk inhibitors.
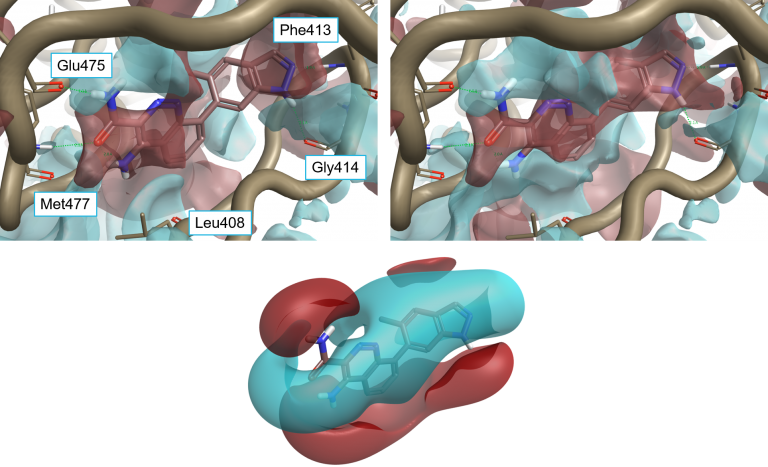
Ligand 4L6 superimposed to the protein interaction potentials of 4Z3V. Top-left: ‘dry’ active site, not including crystallographic water molecules. Top-right: ‘wet’ active site including stable water molecules. Bottom: Ligand fields for 4L6. Protein interaction potentials shown at isolevel = 3; ligand fields shown at isolevel = 2.
Field similarity for ligand-based design
Good-quality electrostatic potentials on a molecule can be computed based on an advanced representation of its underlying charge structure. The next step is being able to compare two conformations in terms of their electrostatic similarity. You can do this just by comparing the field points of the two molecules, which leads to a pharmacophore-like technique. However, a better solution is to take account of the full electrostatic potential.
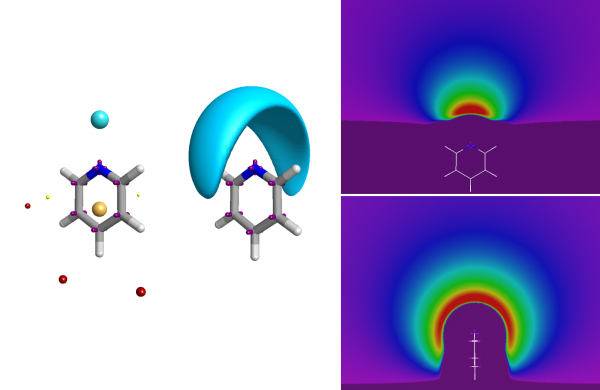
The full electrostatic potential contains more information than just the fact that the nitrogen is an acceptor.
Similarity needs to be computed in terms of the underlying potentials, not just in terms of the field points. Although computationally difficult, Cresset’s solution is both elegant and effective. The fields of the two molecules are compared, but only at the places where one of the conformations has a field point; keeping the number of field computations limited, but ensuring the field is computed only at places where at least one of the conformations suggested that the field was important (i.e., at a field point). The full algorithm has been published (Cheeseright et al JCIM 2006).
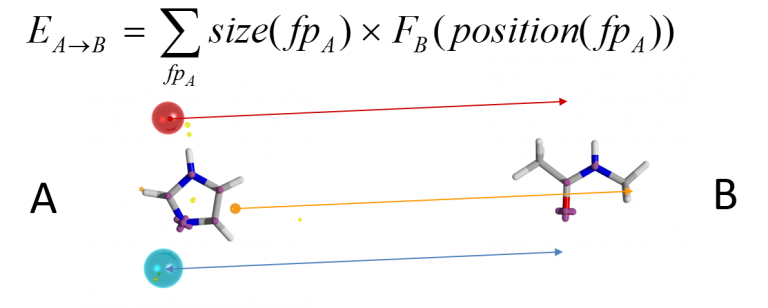
A score for conformation A into conformation B is computed by determining the field potential for B at the places where the field points for A lie. The overall score can be made symmetric by also computing the converse B-into-A score and averaging the two. However, it is not enough to score a particular alignment: you need to be able to locate the optimal alignment. This is a difficult global optimisation problem. Cresset’s solution is to generate a set of initial alignments by computing colored clique matches between the sets of field points on the two conformations: a clique match is a set of field points on each conformation that match in terms of field point type and in terms of all of the inter-field-point distances (to within a distance tolerance). Each clique match determines an alignment (by least-squares fitting of the matching field points in 3D), and the alignments are then scored according to the field similarity algorithm described above. The top-scoring alignment is then taken as the ‘correct’ alignment for those two conformations.
In many cases, of course, it is not known which conformation the molecules should be in. If comparing two known bioactive conformations, for example from protein crystal structures, then the field similarity algorithm can be applied directly. It is more often the case that one of the molecules has an unknown conformation: the best example is virtual screening – searching with a defined 3D conformation of the query molecule, but not knowing a priori if the conformation of the molecules being searched is going to be relevant. In this case a conformation search is performed, generating a set of conformers that represent the available conformational space of the molecule. Each of these are aligned to the query and the best-scoring alignment is taken as the overall score of the molecule.
In some circumstances it is necessary to compare molecules without knowing the bioactive conformation of any of them. In this situation conformer populations are computed of both molecules and compare each conformation of the first to each conformation of the second. This is the procedure that is used in our FieldTemplater technology for pharmacophore elucidation.
The field similarity algorithm is fast. Comparing a query conformation to a set of 100 conformers of a molecule takes 1-2 seconds on a single CPU core. It has proved very effective for virtual screening. Assessment of the performance of Cresset’s similarity algorithm as embodied in our Blaze virtual screening software shows that it performs significantly better than docking (Cheeseright et al JCIM 2008). The algorithm can be enhanced by combining it with a shape similarity calculation (Grant et al): the overall similarity is a weighted combination of the field similarity and the shape similarity. In most cases an equal weight is used (50% shape, 50% fields), but this is customizable by the user for particular circumstances.
Further enhancements of the field similarity calculation include the ability to add field constraints, pharmacophore constraints and excluded volumes. Field constraints are used to mark a particular region of field as being of higher importance than the rest, pharmacophore constraints require particular types of atoms to be close to each other, while excluded volumes enable the use of protein structure information to constrain alignments to lie within the available space. All of these can significantly improve the accuracy of alignment and scoring.
Electrostatic Complementarity™
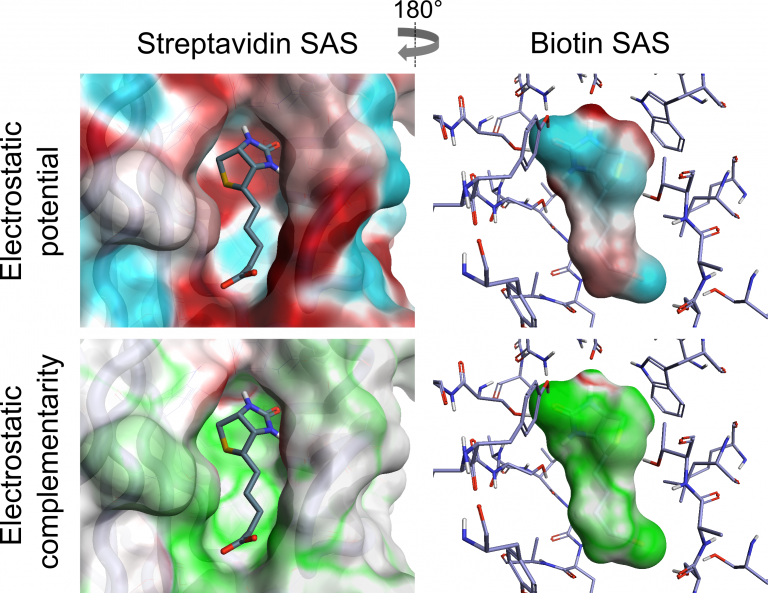
Cresset has combined the analysis of ligand electrostatics with that of protein electrostatics to generate a visual and numerical assessment of the Electrostatic Complementarity (EC) of ligand protein complexes. The Cresset EC method is computationally inexpensive and can be applied to large data sets. We have analysed both the visual and numerical components by applying the method to a range of literature sets, showing that it correlates with and can predict reported bioactivity differences – see our paper in J. Med Chem. EC analysis has also been applied to kinase selectivity prediction, streptavidin mutant analysis and selection of ligand protonation states in protein context. The results of this work have shown that assessing EC can be a powerful tool for analysis and optimization of electrostatic protein-ligand interactions, making it possible to quantify electrostatically driven SAR and predict electrostatic target selectivity. The Cresset protein-ligand EC is calculated from comparison of protein and ligand electrostatic potential (ESP) values at all vertices of a generated ligand or protein solvent accessible surface (SAS) [1,2]. Perfect electrostatic complementarity would mean that at each vertex the ligand ESP value would be paired with a protein ESP value of the same magnitude with reverse sign. Below is a visualization of both ESP and EC of the biotin-streptavidin complex on both ligand and protein SAS, showing how a close matching of positive and negative electrostatic potential areas of protein and ligand leads to a good EC.
Below, we calculate an EC score that provides an approximate correction for some desolvation effects and allows local visualization of EC on a protein or ligand solvent-accessible surface where the integral is over the ligand SAS, ESPL and ESPP, the ligand and protein ESP values, and MAX(ESPL,ESPP,k) the protein or ligand ESP value with the larger deviation from zero, or a constant k if that is larger. Ligand and protein ESP values are capped to the maximum ESP values observed for water molecules to approximately correct for desolvation. EC scores range from 1 to -1, corresponding to a perfect EC or complete electrostatic clash, respectively. As solvent-exposed portions of the ligand contribute less information about the electrostatic complementarity of protein-ligand complexes, regions of the ligand SAS that are more than 3 Å away from any protein atom are scaled down by a distance-dependent factor.
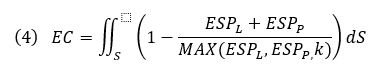
The Cresset EC method has been applied to a reported XIAP-BIR3 data set, demonstrating that this method can detect and quantify electrostatic differences in XIAP ligands that cause changes in bioactivity. See Investigating the SAR of XIAP ligands with Electrostatic Complementarity maps and scores.
References
- Xu, D.; Li, H.; Zhang, Y. Protein Depth Calculation and the Use for Improving Accuracy of Protein Fold Recognition. J Comput Biol 2013, 20 (10), 805–816. https://doi.org/10.1089/cmb.2013.0071.
- Xu, D.; Zhang, Y. Generating Triangulated Macromolecular Surfaces by Euclidean Distance Transform. PLoS ONE 2009, 4 (12), e8140. https://doi.org/10.1371/journal.pone.0008140.
Free energy perturbation at Cresset
Free energy methods are being increasingly widely used in drug discovery as a way of computing the absolute or relative free energy of bonding of ligands to proteins. By simulating the protein and ligand in a box of water, the dynamics of the interactions can be captured giving a more accurate binding energy estimate than cheaper methods such as docking scoring functions or MM/GBSA. In general, relative free energy estimates as significantly easier to compute and more reliable than absolute ones, as we benefit from a cancellation of errors.
Alchemical free-energy calculations for computing the binding energy of a compound A relative to a reference compound B generally involve a thermodynamic cycle in which A is transformed into B in the protein environment and in a simple solvent (Figure 1).
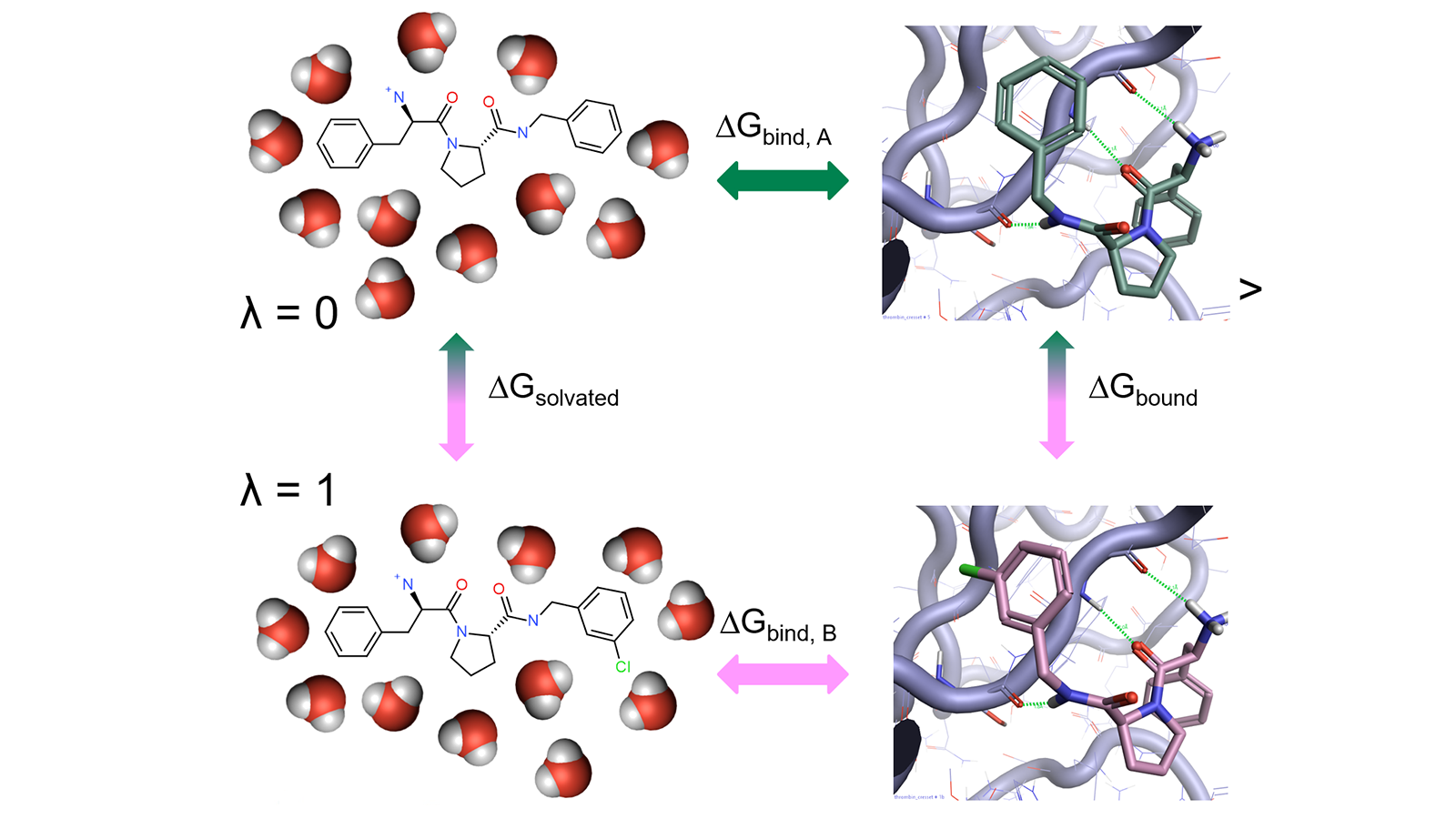
Figure 1: Thermodynamic cycle used in relative free energy calculations.
The corresponding states of A and B need to have significant overlap in their potential energy distributions, as otherwise the configurations sampled for A may be of low probability for B, which leads to slow convergence of the free-energy change and computation of the result may not be possible. This limitation is typically overcome by introducing a coupling parameter λ which takes on values between 0 and 1 to interpolate the potential energy functions of the end states. The transformation from A to B is then achieved through a varying number of artificial ('alchemical') states characterized by intermediate λ values (the so-called λ-windows) providing an improved overlap of potential energy distributions between neighboring states. (Figure 2).
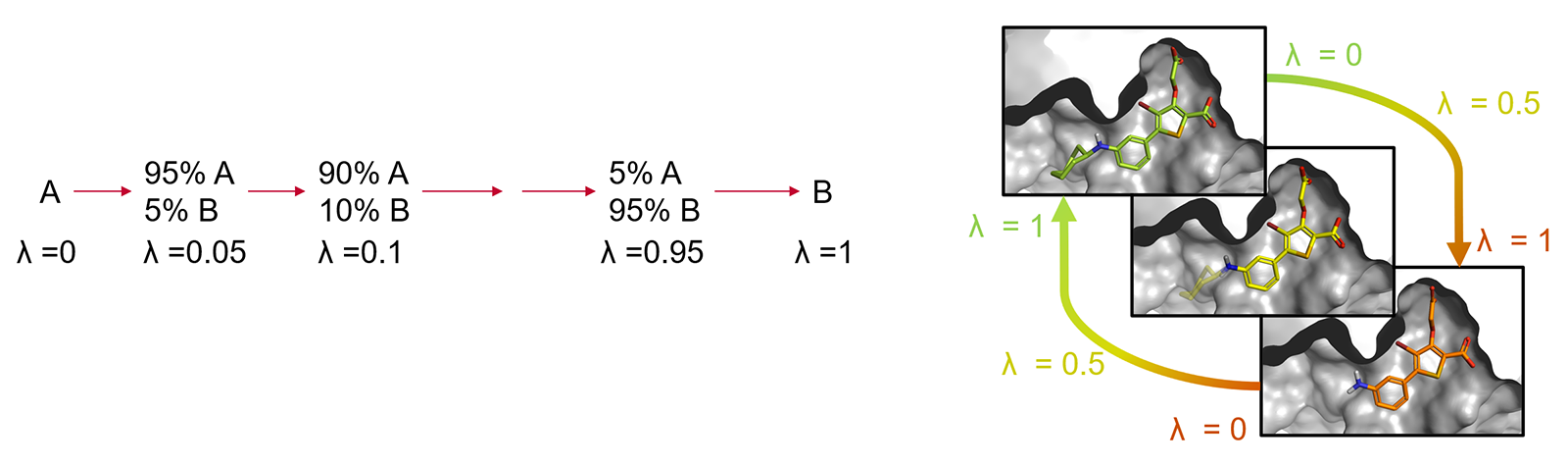 Figure 2: Alchemical transformation of ligand A to ligand B via a series of nonphysical intermediates.
Figure 2: Alchemical transformation of ligand A to ligand B via a series of nonphysical intermediates.
Cresset’s implementation of relative free energy calculations is based on a suite of open-source tools (Figure 3), in particular the SOMD module of the SIRE toolkit. The SOMD package has been previously successfully applied to relative and absolute binding free energy studies of a range of fragments, drug-like small molecules, carbohydrates, and host−guest systems.
 Figure 3: Open source tools used by Flare FEP.
Figure 3: Open source tools used by Flare FEP.
The results of using Flare FEP on the standard data set of Wang et al. (J. Am. Chem. Soc. 2015, 137, 2695−2703) are shown in Figure 4 and Figure 5. For more details on the methods used in Flare FEP and how this benchmark was carried out see our paper (Kuhn et al., Journal of Chemical Information and Modeling 2020 60 (6), 3120-3130).
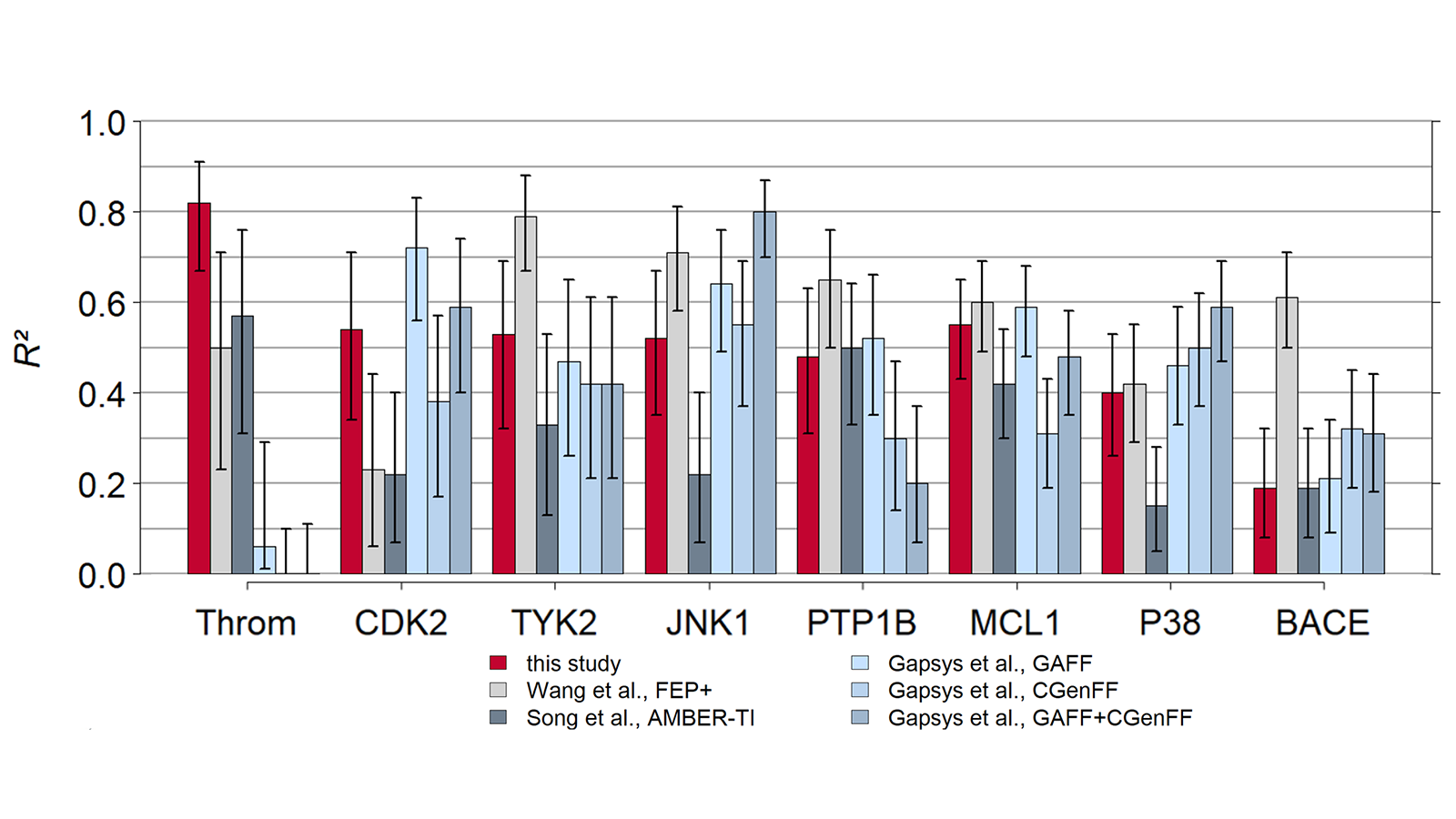
Figure 4: Correlation of predicted vs actual activity.
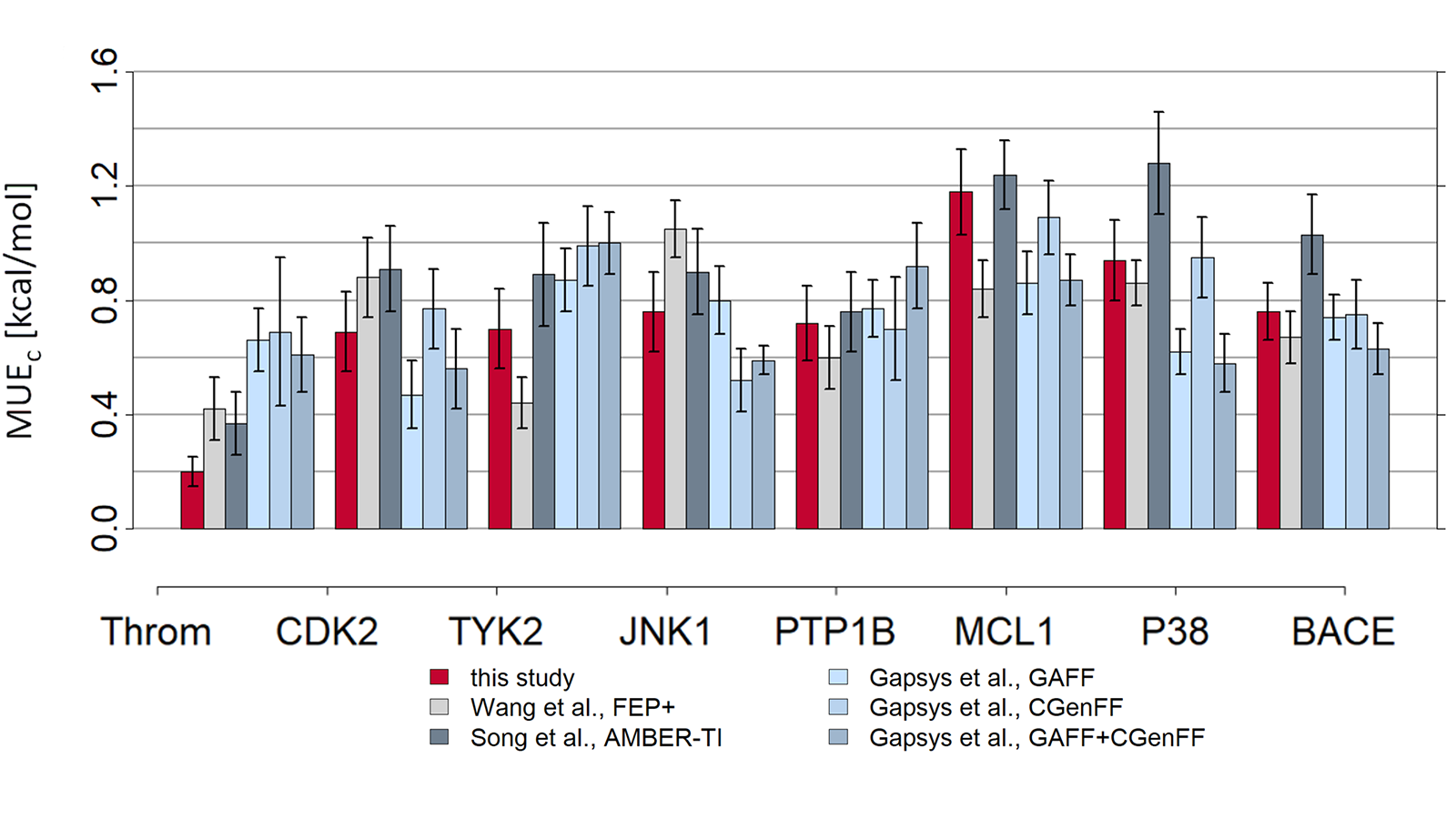 Figure 5: MUE of predicted vs actual activity.
Figure 5: MUE of predicted vs actual activity.
One of the more complex parts of setting up an FEP calculation is creating the network that defines the transformations between the molecules. As FEP calculations are most reliable and accurate when computing the relative activity of closely-related molecules it is important to set up a network with care. Ideally the FEP network should adhere to the following guidelines:
- Each molecule should be connected with at least two others within the network, to provide redundancy.
- The connections should link molecules that are closely-related.
- All molecules should be in a small cycle to facilitate cycle closure analysis and consequently identify potential errors.
- The overall diameter of the graph should be kept relatively small to avoid the risk of systematic errors propagating from one end to the other.
Flare uses a modified version of the LOMAP tool to perform this analysis, resulting in graphs like the one shown in Figure 6. The LOMAP procedure has been optimised to align its scores to the known behaviour of our FEP method, to allow 3D coordinates to inform the atom mapping, and to correctly handle chirality inversions between molecules.
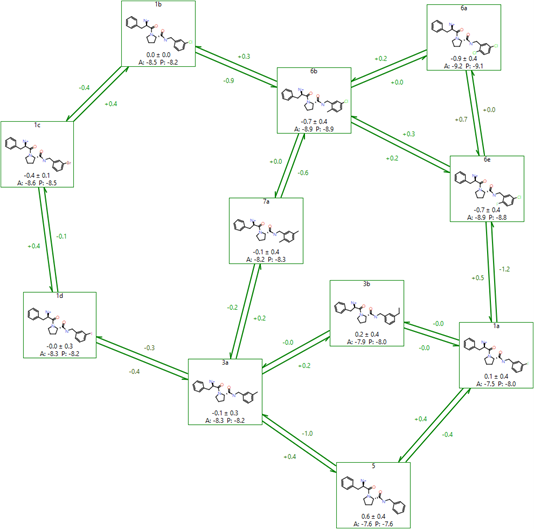
Figure 6: An example FEP network created by LOMAP in Flare.
The optimal schedule of λ values for each link is determined using a short precalculation (Figure 8). This procedure allows a set of λ values to be obtained that keeps good phase space overlap between the simulations while minimising the number of calculations. In testing this generally resulted in a 30% decrease in the number of λ window simulations that needed to be performed.
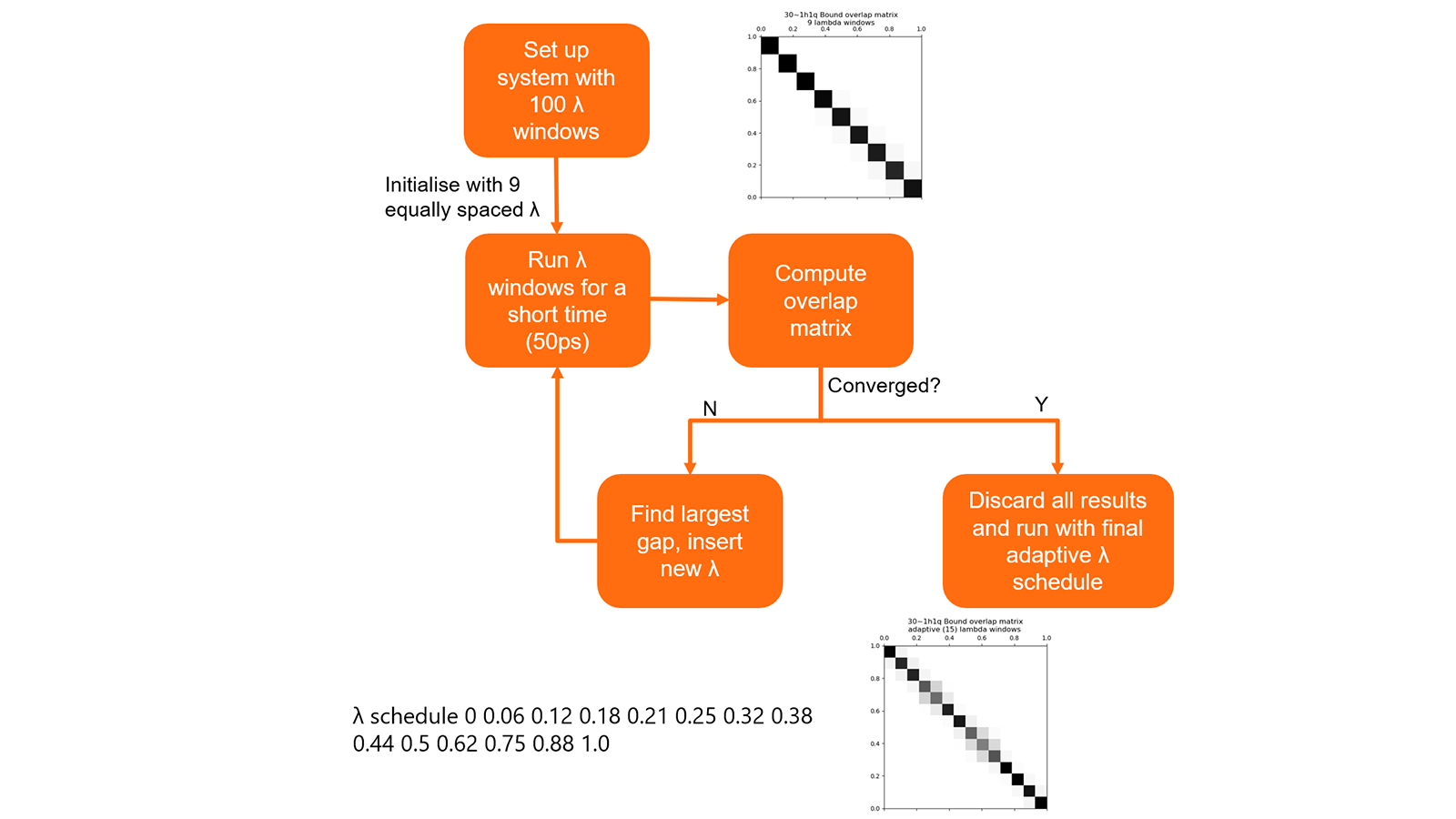
Figure 7: Summary of algorithm to determine optimal λ schedules for links.
In some cases, the nearest neighbours to a particular ligand might be too far away to allow for efficient calculation. Flare FEP works well with up to 8-9 atom differences between ligands, although this number is reduced if the added or removed atoms are highly polar. In cases where the near neighbours have differences larger than this, it is generally useful to introduce intermediate structures as better ΔΔG estimates will be obtained from two chained conservative links than from one ambitious one. In Flare FEP, a heuristic algorithm automatically generates and inserts to the FEP graph sensible intermediate structures (Figure 8).
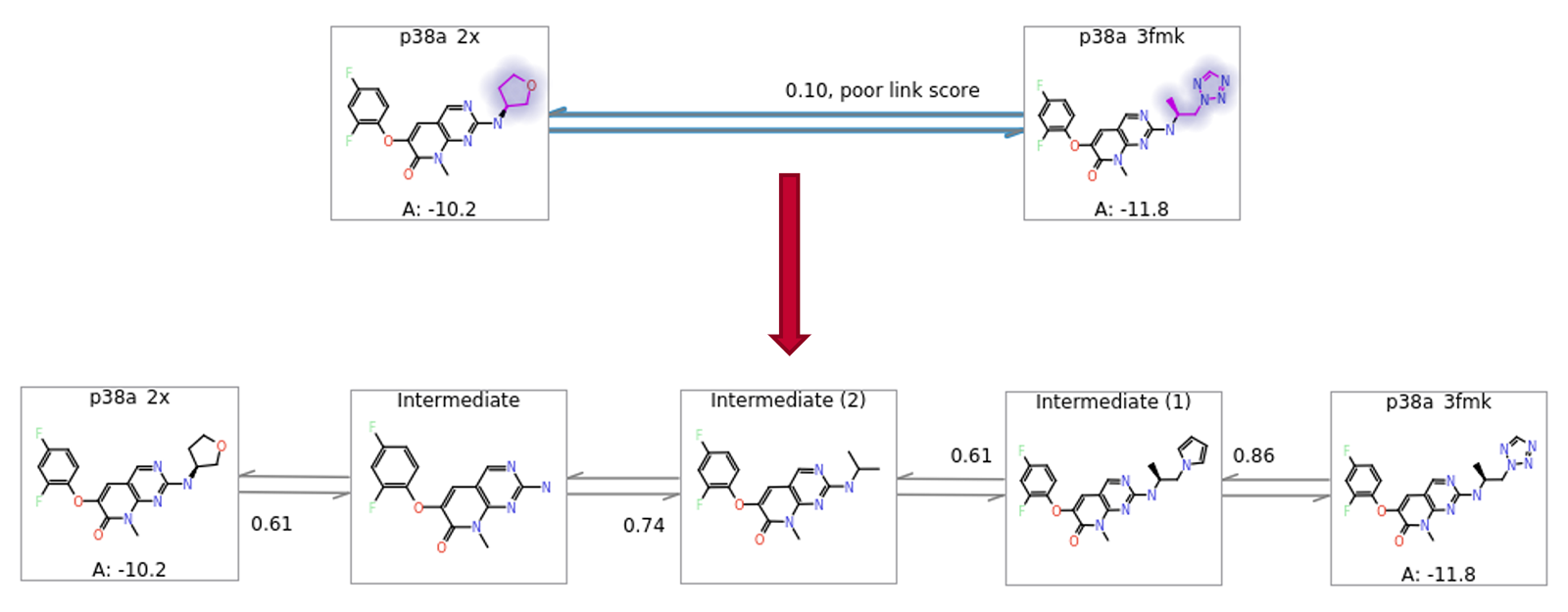
Figure 8: Automatic addition of intermediates to allow more robust estimation of ΔΔG for large changes.
3D virtual screening using Ignite™
Ignite™ is a new technology to enable rapid 3D virtual screening in combinatorial chemical spaces. Conventional virtual screening on large data sets is typically carried out by comparing molecular fingerprints. This makes screening relatively fast but has the drawback that top-scoring results are less likely to be actual hits. Molecules are three-dimensional in nature, of course, and therefore a 3D descriptor for molecules can lead to more reliable hit detection. The Ignite 3D descriptor uses Cresset field technology 1 which describes a molecule through its spatial extent of electrostatics and its shape for a given conformation.
Synthesizable chemical spaces are vast and routinely contain billion of molecules 2. This means that fully enumerated libraries would require prohibitively large storage space and computational resources to search through this space. A much more practical approach, therefore, is to utilise the combinatorial nature of most chemical spaces i.e., a relatively small number of building blocks/fragments is combined to create a much larger number of enumerated compounds. One such example is Enamine REAL Space which, at the time this was written, boasts 24 billion possible compounds which have a high probability, of around 80%, to be synthesizable.
The Ignite algorithm solves the problem of searching through such large spaces by performing a fast initial screen in reagent space. Reagents for each virtual library are converted into ‘product-like’ fragments, converting their reacting functional groups into minimal representations of the library products. These product-like fragments are then screened against the query molecule to determine which ones are likely to provide significant shape and electrostatic similarity.
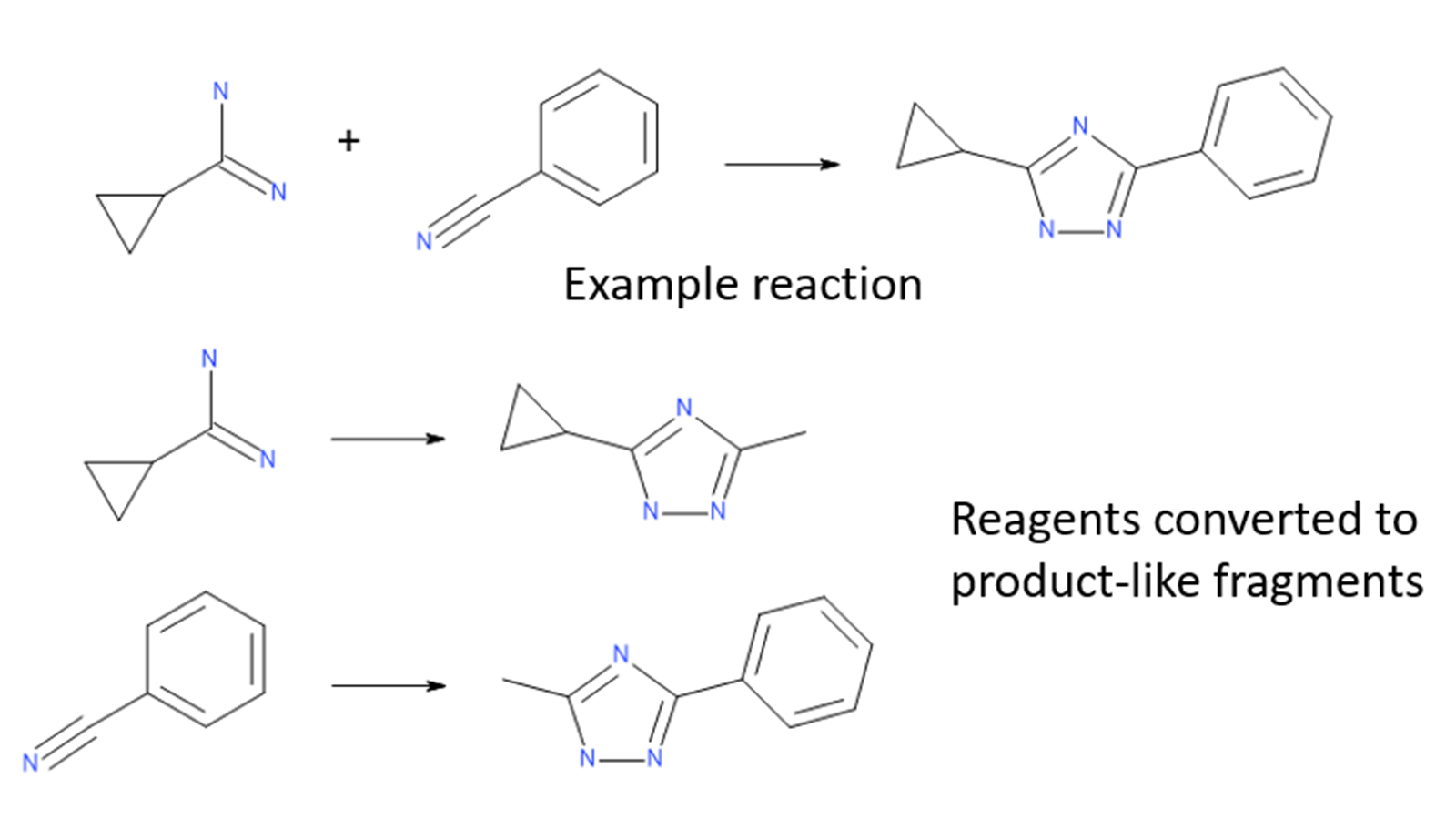
Figure 1: Library reagents are converted to product-like fragments for each reaction.
Only the highest-scoring fragments are passed through to the next stage, where they are combined using Spark™ technology with the synthons from the other half of the reagent space. The combined molecule is then overlayed with the query molecule and scored again. This strategy is depicted in Figure 2.
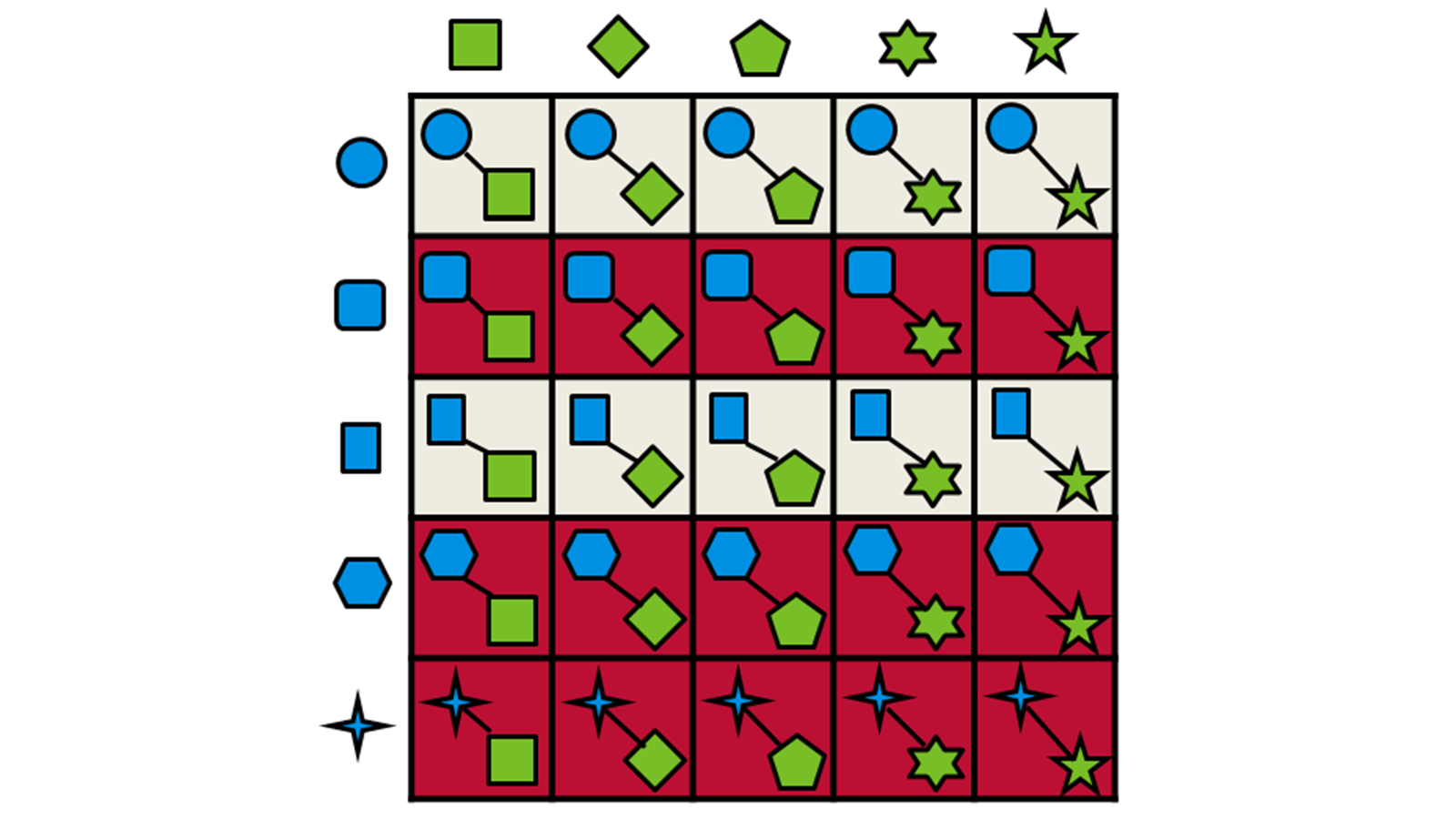
Figure 2: Schematic representation of the fragment combination and product selection process used by Ignite.
The table below compares enrichment factors obtained by Ignite and Blaze™. Blaze is a ligand-based solution for 3D virtual screening that operates in enumerated space, so is suitable for libraries of millions of molecules. On a validation library space of a million molecules we compared the results retrieved with Blaze to those obtained using the much more rapid Ignite method. The results show that Ignite can retrieve a high proportion of the Blaze hits while screening only a tiny fraction of the total chemical space. Application of Ignite to larger spaces yields even better performance: in the hands of our validation partner Bayer a full Ignite screen across the Enamine compound collection (>10Bn molecules) can be achieved in less than four hours on 100 CPUs.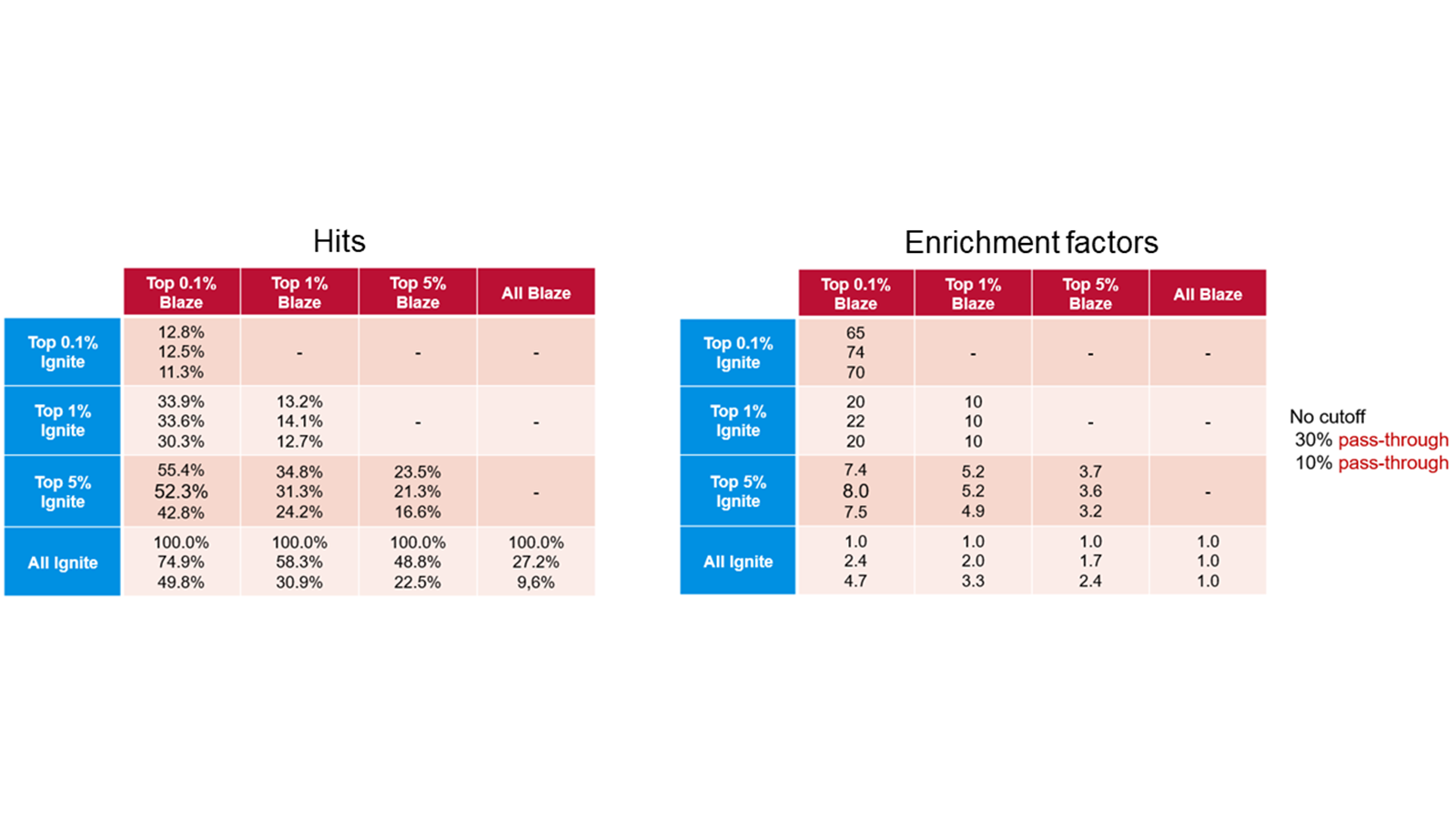
Table 1. Ignite results (left) and enrichment factors (right) using Blaze results as the baseline.
Apply the power of Ignite to your project
Ignite can be applied to your project by outsourcing to Cresset Discovery who have an expert team of computational chemists ready to help you accelerate creation of your commercial assets. Contact Cresset Discovery for a free confidential discussion to explore this further.
- Cheeseright, T; Mackey, M; Rose, S; Vinter, A. J; Molecular Field Extrema as Descriptors of Biological Activity: Definition and Validation, J. Chem. Inf. Model. 2006, 46, 2, 665-676. http://dx.doi.org/10.1021/ci050357s
- Warr, W. A.; Nicklaus, M. C.; Nicolaou, C. A.; Rarey, M.Exploration of Ultralarge Compound Collections for Drug Discovery, J. Chem. Inf. Model. 2022, 62, 9, 2021-2034. https://doi.org/10.1021/acs.jcim.2c00224