Virtual Screening Strategies for Identifying Novel Chemotypes
In their recent article in Journal of Medicinal Chemistry, Stuart Lang and Martin Slater review in silico approaches for identifying ...
News
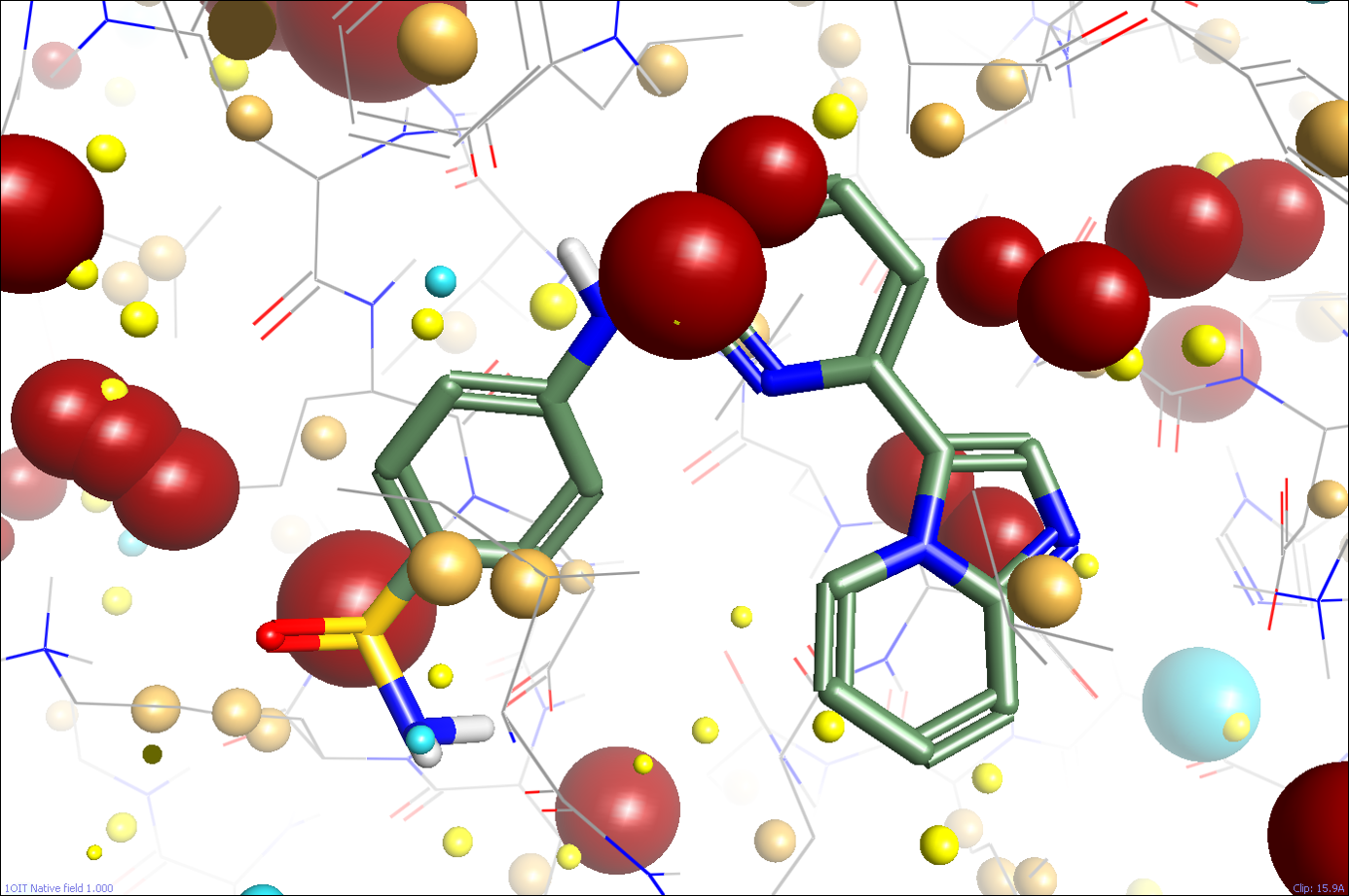
Last month, I looked at how Cresset calculates molecular electrostatic fields on ligands. So, can we perform the same calculations and place a field on a protein? Of course we can! Figure 1 shows the protein field in the active site of CDK2 (pdb: 1oit) calculated using our standard field calculation methods (the ligand is shown for reference, but the field points are all from the protein). The field points are all there, but they don’t look that useful. The active site is swamped in huge positive field points, with no negative ones at all.
So what went wrong? As you may recall from last month, the problem of calculating useful molecular electrostatics for ligands was more complex than it at first seemed: you need to think carefully and deeply about the expected environment of the ligand in order to get results that make sense. In particular, we use a quite low dielectric environment, but applied a higher dielectric constant for formally charged groups on the grounds that we expect these to either be solvated or to be binding in a part of the protein with high charge mobility or a counter-ion present.
For the ligand, assuming that it’s embedded in a low dielectric environment is quite reasonable. However, this is quite wrong for the protein, which is fully solvated by water. Should we instead be slapping a dielectric of 80 on it, or taking the time to do a proper Poisson-Boltzmann solvation calculation? Either of those would improve the situation, but first we need to step back and consider why we want to calculate fields on proteins in the first place. We’re primarily interested in protein fields for what they can tell us about potential ligands. This may change in the future if we want to look more closely at protein-protein interactions, but in the meantime it’s the field in the (generally small and partially enclosed) active site that is of interest, not the whole protein.
The solution to getting good fields on the ligand was to consider their environment, so the solution to getting useful field maps of protein active sites is their environment. If we want to compare two protein active sites to each other using fields, we generally want to do so in the context of a ligand (is the same ligand going to bind to both proteins?), not in the context of the apo proteins. So the question of the dielectric environment is again much more complicated than it at first appeared. The protein active site isn’t a vacuum, but neither is it generally fully solvated by water: any water present is confined and has limited similarity with bulk water, and in any case the active site will have a ligand of some sort in it.
So, maybe for our local environment within the active site our existing low-dielectric assumption might not be too bad after all. However, it’s a very poor model for the rest of the protein, which is likely to have multiple highly-charged residues partly or fully solvated by water. That’s why the field pattern shown in Figure 1 is so useless – it’s dominated by the bulk of the protein, and not by the local environment around the active site (remember that electrostatic fields only fall off as 1/r, so a charged residue 15Å away can have a big effect on the local electrostatics!).
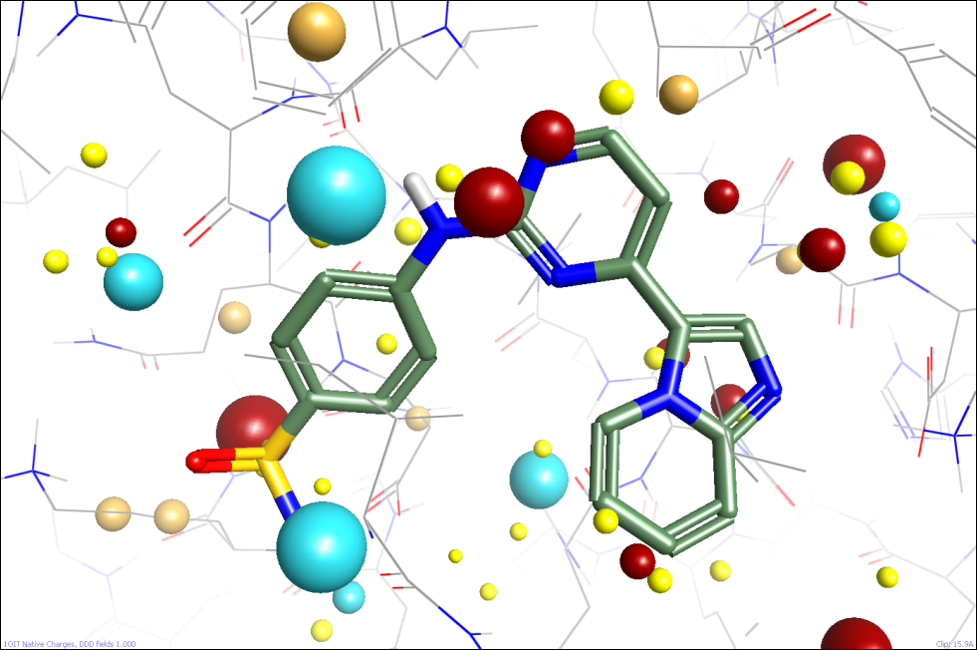
We’re looking at several ways of approaching this. One option might be to apply a Poisson-Boltzmann-like solvation model, but we’d want to apply that to most of the protein but not the active site itself. Defining the boundary is going to be difficult, and PB solvers are slow, so we’re not pursuing that currently. Instead, we’re seeing whether numerically simpler methods can give us useful results. The first simple approximation we can make is to apply a distance-dependent dielectric. This allows the electrostatic field in the active site to strongly reflect the local environment while reducing the impact of more distant residues (figure 2). One disadvantage of this approach is that while it helpfully reduces the effect of solvated charged residues on the surface of the protein, it also unhelpfully reduces the effect of alpha helix dipole moments and the like.
The second simple approximation we are looking at is analogous to the additional dielectric that we apply to charged functional groups on ligands. We estimate how solvent-accessible charged residues are, and apply a separate dielectric to each based on this estimate. Fully-solvated residues get a dielectric of ~80, while fully-buried ones get ~4. Again, this seems to work reasonably well on initial testing, allowing the fields of the active site to be analysed without being swamped by the overall formal charge of the protein (figure 3).
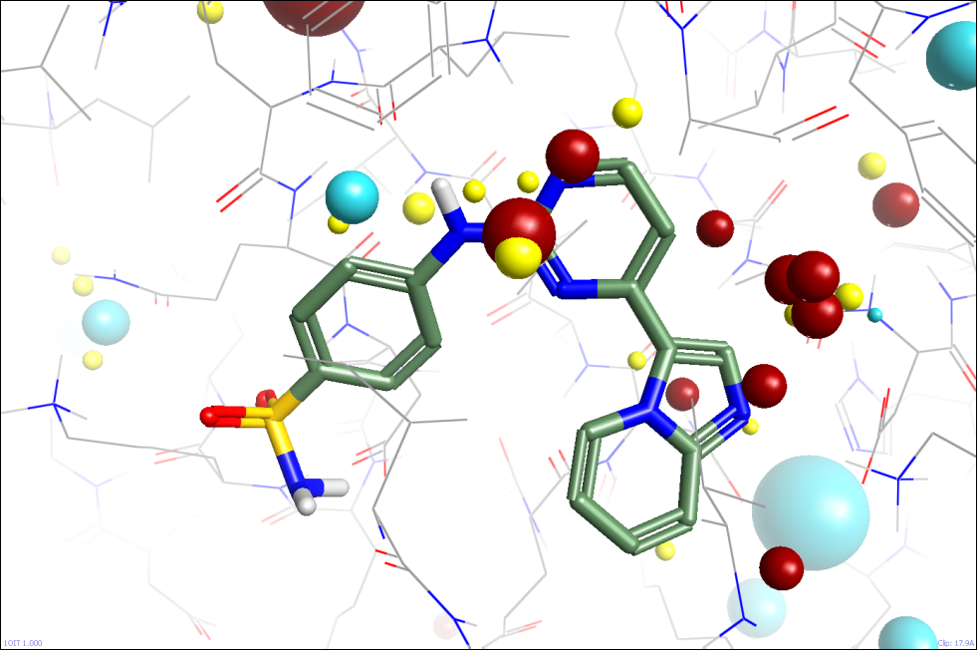
This method is arguable more of a fiddle as we apply this ‘solvation’ metric only to formally charged groups and not to the rest of the solvated residues, but it’s simple, fast, and seems to perform well.
We’re currently actively evaluating both of these methods (and a couple of other ideas) in order to find out how we can best generate field patterns for protein active sites. This will have two major benefits for our customers. Firstly, having a realistic way of comparing the shape and electrostatic properties of two protein actives sites will be very useful in working out which proteins might be similar to the target for a drug discovery program, and hence in designing cross-screens to ensure that no undesired cross-target activity creeps in during lead optimization. Secondly, having a good picture of the protein active site fields will allow us to alter our ligand field similarity algorithms to put more weight on those regions of the ligand which make stronger interactions with the protein.
We’ll be presenting some of the results from our protein field comparisons later this year, so stay tuned!