News

Pharmacophore constraints – when should they be used?

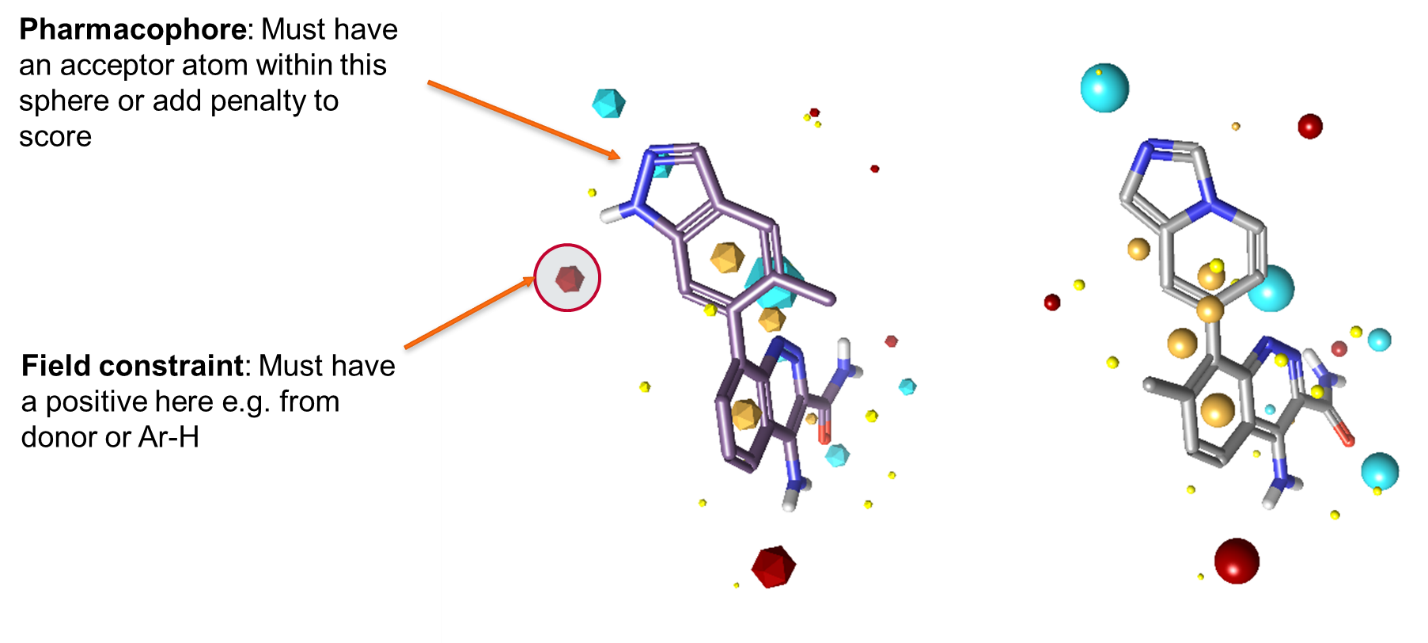
Cresset’s alignment and scoring technology is based around the idea of electrostatic matching: the ‘best’ alignment of a pair of conformations is generally the one that provides the most similar molecular interaction potentials. In most cases this is true. However, we recognize that often some portions of the electrostatic potential, for example those involved in a strong hydrogen bond, can be more important than others. This isn’t information intrinsic to the molecules themselves, but to the context in which they are being used. As a result, we have for many years offered the possibility of adding ‘field constraints’, which force the alignment algorithm to prioritize matching the electrostatic potential in particular places around a ligand.

It’s worth noting that the field constraint algorithm works by applying a score penalty to alignments which violate the constraint, not by forcing the constraint to be matched (Figure 1). In general, soft constraints delivered via score penalties are preferred to hard constraints where we simply disallow alignments that violate the constraint. There are two reasons behind this. Firstly, using a score penalty allows the strength of the constraint to be adjusted, so that it can be anything from a mild hint to a strict requirement. Second, in most cases we feel that it is better to get a best-effort alignment that violates the constraint than nothing at all, especially when using the algorithms in lead optimization and trying to align a set of known actives.

Figure 1: Field constraint requires the field at the position of a particular field point to have a certain minimum value.

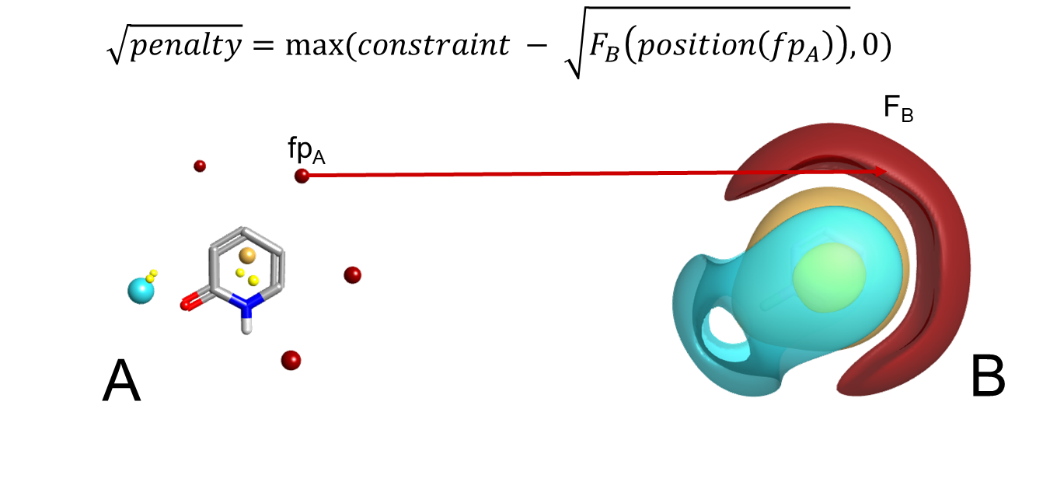
While field constraints work extremely well in the majority of cases, there are a few exceptions. In some cases there isn’t a field point at the place you want to add a constraint (although this problem is alleviated by the new field editor in Forge and Spark). More commonly, the constraint that you want to add is either stronger or more specific than can be expressed through fields: sometimes generic positive potential isn’t enough and you want to explicitly require a hydrogen-bond donor, for example, and sometimes you want to ensure that the metal-chelating group in a set of ligands is aligned, and ‘good metal chelator’ is similarly difficult to pin down in terms of pure electrostatics. In addition, the donor-acceptor motif that is often required in the hinge binding region of kinases can be difficult to describe through fields alone, as the donor and acceptor electrostatics cancel out to some extent making this region contribute less to the overall alignment score than it should.

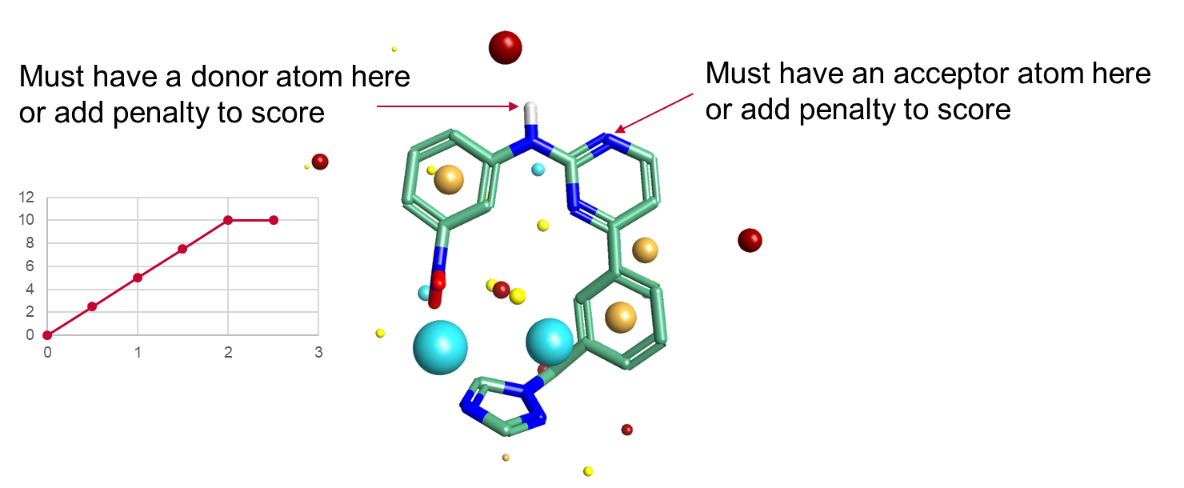
For these reasons we introduced the option of pharmacophoric constraints to our core algorithms. These operate in a similar fashion to field constraints, in that they are constraints not requirements. Traditional pharmacophore algorithms treat pharmacophores as binary switches: you either have a H-bond donor in a region of space, and hence a full match, or you don’t and therefore don’t have a match. Our pharmacophore constraints instead operate on a sliding scale. You specify how strong the constraint is, and hence how much alignment score should be lost if the constraint is not satisfied. We spent a while looking at what form the penalty function should take, and the best form overall was a simple linear penalty with a cap at 2Å distance (Figure 2).

Figure 2: Pharmacophore constraints require an atom of the specified type to be within 2Å of the constrained atom, or a penalty is applied to the score.

We’ve talked elsewhere about the validation of our pharmacophore constraints on virtual screening performance within Blaze, where for some targets they can make a significant difference. However, the new constraints are useful for more than just virtual screening. What effect does adding constraints have on the probability of a successful ligand alignment?

We investigated this by using the standard AZ/CCDC dataset from Giangreco et al. (J. Chem. Inf. Model. 2013, 53, 852−866), which contains a large number of targets, and for each target a collection of aligned co-crystallized ligands. The data set can be used to validate ligand alignment algorithms, by measuring what proportion of the ligands within a target class can be successfully aligned. However, running a validation over the entire data set would be challenging, as it would pose the question for each target as to what pharmacophore constraints should be applied. We decided to address this by only testing (in the first instance) 4 kinase targets, as the donor-acceptor-donor motif for kinases is well understood and fairly uncontroversial. For each ligand in these 4 target sets, we manually applied between 1 and 3 pharmacophore constraints to the hinge binding region based on how many H-bonds were actually made by that ligand. For the purposes of this experiment we only included ‘true’ H-bonds from hydrogens on O or N, not the weaker C-H form. Note that all of the alignments were performed in ligand space only, with no information from the proteins applied.

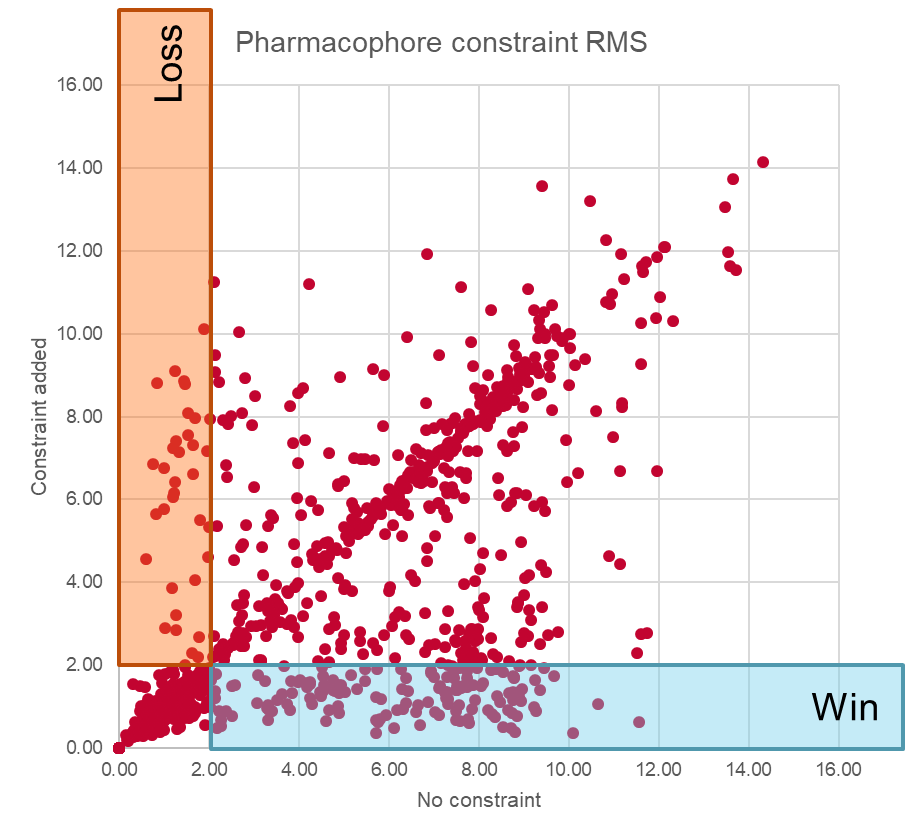
The distribution of results is shown in Figure 3. We used a cutoff of 2Å to distinguish between correct and incorrect alignments. As can be seen, a significant number (around 13%) of alignments that were incorrect when unconstrained were rescued by adding the constraints – that’s a significant improvement. However, at the same time, around 3% of the alignments that we had been getting correct were made worse by adding the constraints, and it’s also apparent that there are a number of incorrect alignments which are left unchanged by the imposition of constraints. Overall the pharmacophores are a net win, especially for these kinase data sets, but it’s not a magic bullet.

Figure 3: Effect of adding pharmacophore constraints to 4 kinase alignment data sets. The alignments in the ‘Win’ section are improved by the addition of constraints, while those in the ‘Loss’ section are made incorrect.

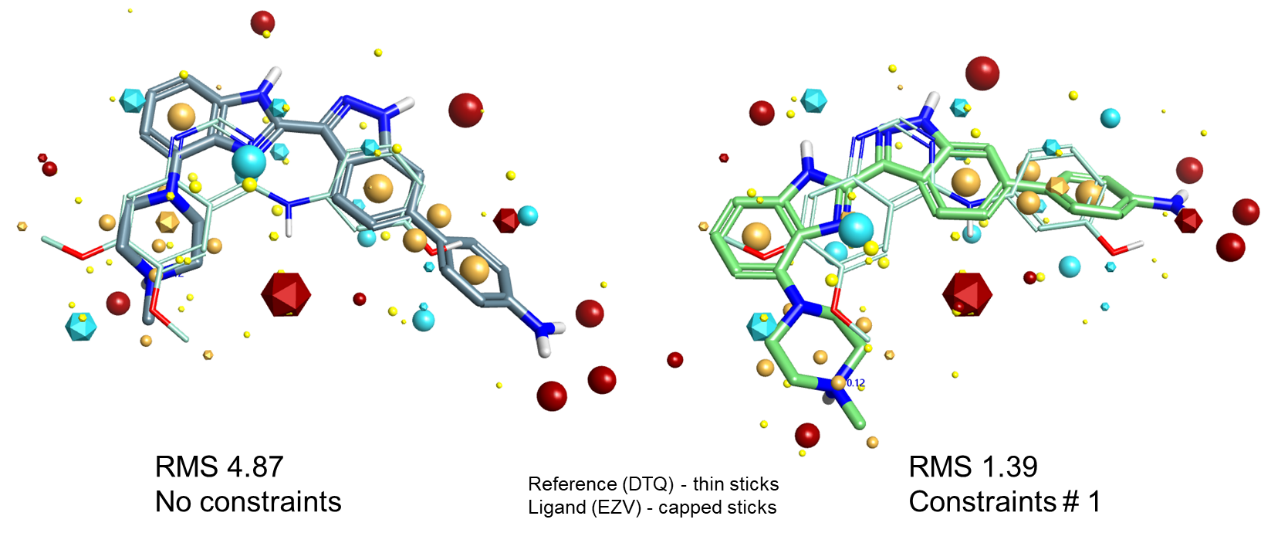
Let’s look at a couple of examples. Figure 4 shows a case where adding hinge binder constraints converts an incorrect alignment to a correct one. The unconstrained result on the left matches the dimethoxyphenyl ring on the left and the phenol on the right very well, but at the expense of the quinazoline nitrogen which makes the hinge interaction. Adding a single acceptor constraint to that nitrogen switches the best solution to one where the indazole nitrogen satisfies the constraint, which happens to be the experimentally-observed alignment.

Figure 4: CDK2, aligning EZV to DTQ.

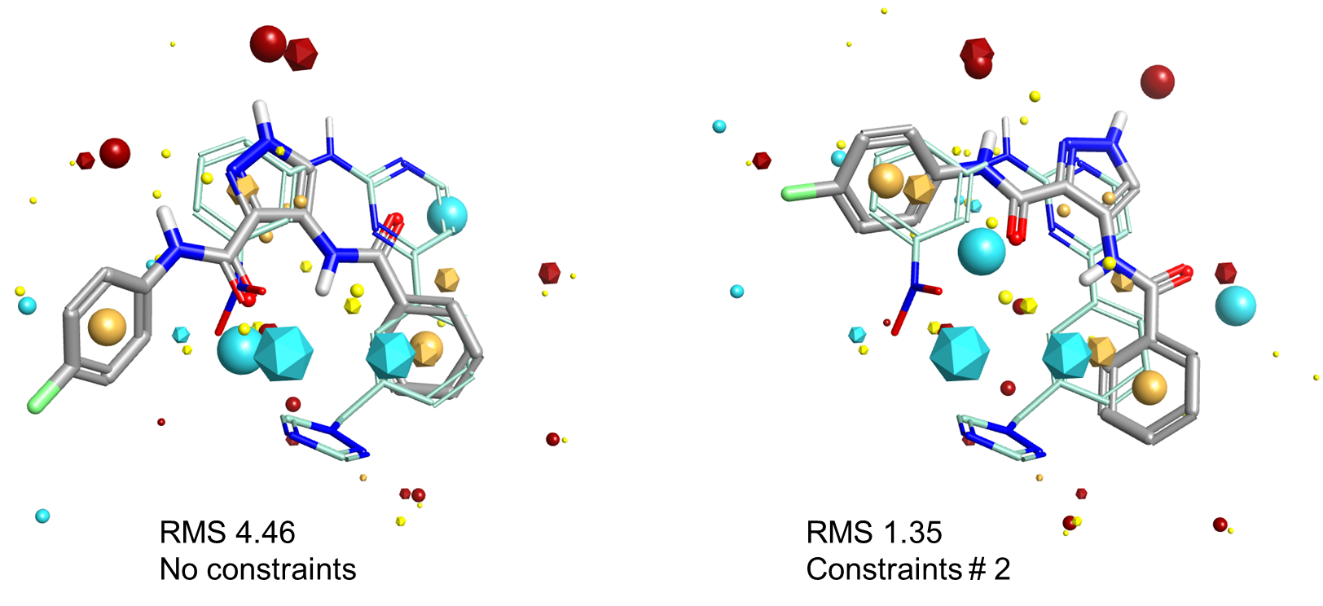
Similarly, in Figure 5, the best alignment in terms of raw shape and electrostatics of MTW and LZ8 is shown on the left. The 2-aminopyrimidine in MTW which makes the hinge interactions is partially matched by LZ8’s pyrazole and carbonyl, but the alignment in that part of the molecule isn’t that good. However, the alignment matches the phenyl ring in both molecules beautifully. Applying a donor/acceptor pharmacophore constraint pair forces the alignment algorithm to try and match the 2-aminopyrimidine much more closely, which leads to the correct alignment on the right. However, note that the phenyl rings are much more poorly aligned.

Figure 5: CDK2, aligning LZ8 to MTW.

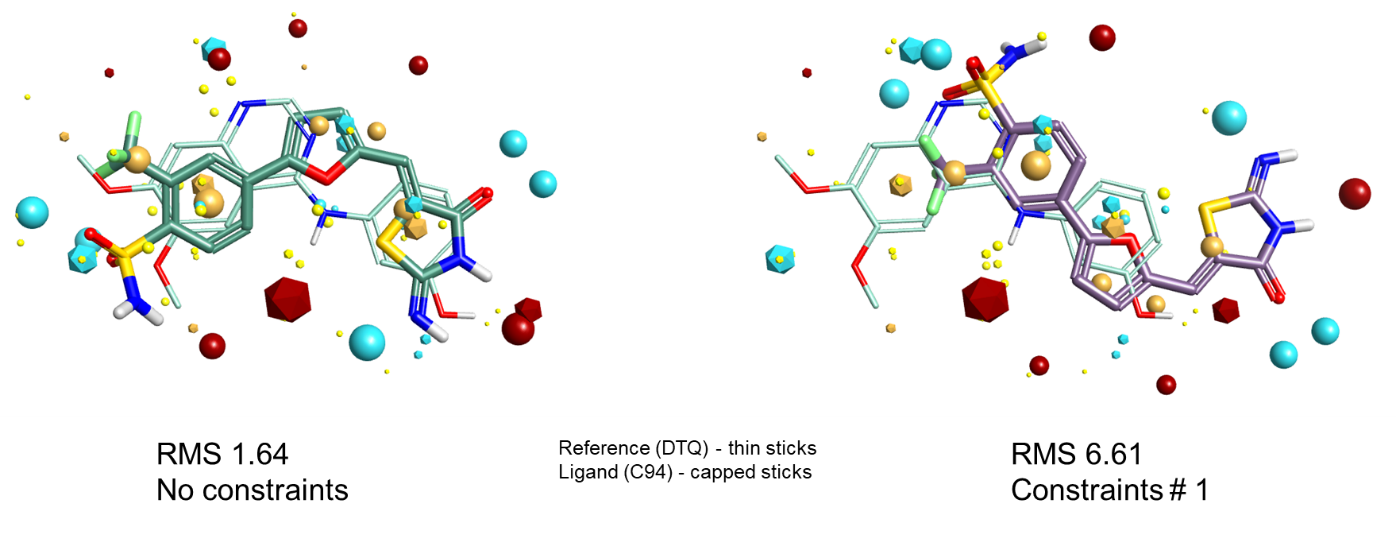
Finally, Figure 6 shows a case where adding field constraints converts a correct alignment to an incorrect one. When aligning to DTQ as the reference, as in Figure 4, the field/shape alignment gets the correct alignment for C94. However, C94 does not make the hydrogen bond to the hinge that we have constrained in the reference. The constraint coerces the alignment to be flipped so that one of the sulfonamide oxygens matches the H-bond acceptor requirement, thus forcing the wrong answer to be obtained.

Figure 6: CDK2, aligning C94 to DTQ.

Pharmacophore constraints can, as you can see, be very useful. If you know that particular interactions are required by the protein, you can provide our tools with that information to help them find the correct alignment. However, it must be kept in mind that by adding these constraints you are adding bias to the experiment: you are nudging it to provide the answers that you expect. Sometimes, the unexpected answers turn out to be correct! We recommend, therefore, that pharmacophore constraints are used sparingly. I personally will always run an unconstrained alignment experiment as a control, just to see if Forge will find an alignment that I hadn’t expected but which might illuminate a previously-puzzling piece of SAR.

So, when should you use a field constraint and when a pharmacophore constraint? The answer depends both on your requirements and on the chemistry inside the active site. If there’s a pharmacophoric interaction that you are certain must be preserved, then using a pharmacophore constraint is probably justified. However, if the interaction is not always present in the same form, a field constraint may be more appropriate. Figure 7 shows a BTK example. The ligand on the left makes two hydrogen bonds to the backbone from the indazole. We might be tempted to add pharmacophore constraints to both the donor and the acceptor, except that there are known highly-active ligands which make a C-H hydrogen bond instead (see the ligand on the right). As a result, it is probably more appropriate, if constraints are required, to add a pharmacophore constraint to the acceptor nitrogen, but use a field constraint to indicate a donor preference in the NH/CH location.